解:(1)令y=0,则x
2-4x+k=0,
解得x=

=2±

,
∵A在B的左边,
∴点B的横坐标x
B为2+

,
∵5<x
B<6,
∴

,
解不等式①得,k<-5,
解不等式②得,k>-12,
所以,k的取值范围是-12<k<-5;
(2)如图,过点A作AG⊥BC于G,作CH⊥AB于H,
∵tan∠ACB=

,
∴设AG=4a,CG=3a,
根据勾股定理,AC=

=
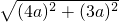
=5a,
∵C为二次函数的顶点,
∴BC=AC=5a,
∴BG=BC-CG=5a-3a=2a,
在Rt△ABG中,AB=

=

=2

a,
∵C为二次函数的顶点,
∴BH=

AB=

×2

a=

a,
在Rt△BCH中,CH=

=

=2

a,
∴AB=CH,
∵AB=(2+

)-(2-

)=2

,
CH=

=k-4,
∴2

=k-4,
两边平方得,16-4k=k
2-8k+16,

整理得,k
2-4k=0,
解得k
1=0,k
2=4;
(3)k=0时,y=x
2-4x,
令y=0,则x
2-4x=0,
解得x
1=0,x
2=4,
∵A在B的左边,
∴点B的坐标为(4,0),
∴OM=4-m,ON=4+n,
∵点D、E都在二次函数y=x
2-4x的图象上,
∴DM=(4-m)
2-4(4-m),
EN=(4+n)
2-4(4+n),
∵△ODE的内心在x轴上,
∴∠DOM=∠EON,
又∵∠DMO=∠ENO=90°,
∴△DOM∽△EON,
∴

=
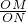
,
即

=

,
整理得,4-m-4=4+n-4,
所以,m+n=0.
分析:(1)令y=0,把k看作常数,解关于x的一元二次方程,得到点B的横坐标,再列出不等式组,然后求解即可;
(2)过点A作AG⊥BC于G,作CH⊥AB于H,根据∠ACB的正切值设AG=4a,CG=3a,利用勾股定理列式求出AC=5a,根据二次函数的对称性可得BC=AC=5a,求出BG=2a,再利用勾股定理列式表示出AB=2

a,然后表示出BH=

a,再利用勾股定理列式表示出CH=2

a,然后根据二次函数的性质表示出AB、CH并列出方程求解即可得到k的值;
(3)先求出点B的坐标,再表示出OM、ON,并根据二次函数解析式表示出DM、EN,根据△ODE的内心在x轴上可知∠DOM=∠EON,然后求出△DOM和△EON相似,根据相似三角形对应边成比例列式整理即可得解.
点评:本题是二次函数综合题型,主要考查了抛物线与x轴的交点问题,解一元一次不等式组,二次函数的对称性,锐角三角函数的正切值,勾股定理的应用,三角形的内心是角平分线的交点,相似三角形的判定与性质,综合性较强,(2)列出根据顶点C的纵坐标和AB的长度列出方程是解题的关键,(3)根据△ODE的内心在x轴上得到∠DOM=∠EON是解题的关键.


 ,求k的值;
,求k的值; =2±
=2± ,
, ,
, ,
, ,
, =
=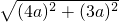 =5a,
=5a, =
= =2
=2 a,
a, AB=
AB= ×2
×2 a=
a= a,
a, =
= =2
=2 a,
a, )-(2-
)-(2- )=2
)=2 ,
, =k-4,
=k-4, =k-4,
=k-4,
 =
=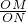 ,
, =
= ,
, a,然后表示出BH=
a,然后表示出BH= a,再利用勾股定理列式表示出CH=2
a,再利用勾股定理列式表示出CH=2 a,然后根据二次函数的性质表示出AB、CH并列出方程求解即可得到k的值;
a,然后根据二次函数的性质表示出AB、CH并列出方程求解即可得到k的值;

 同步拓展阅读系列答案
同步拓展阅读系列答案 24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
