
 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,则四边形OCED的面积为2$\sqrt{3}$.
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2,则四边形OCED的面积为2$\sqrt{3}$. 分析 连接OE,与DC交于点F,由四边形ABCD为矩形得到对角线互相平分且相等,进而得到OD=OC,再由两组对边分别平行的四边形为平行四边形得到ODEC为平行四边形,根据邻边相等的平行四边形为菱形得到四边形ODEC为菱形,得到对角线互相平分且垂直,求出菱形OCED的面积即可.
解答 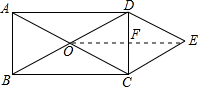 解:连接OE,与DC交于点F,
解:连接OE,与DC交于点F,
∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD,即OA=OB=OC=OD,
∵OD∥CE,OC∥DE,
∴四边形ODEC为平行四边形,
∵OD=OC,
∴四边形ODEC为菱形,
∴DF=CF,OF=EF,DC⊥OE,
∵DE∥OA,且DE=OA,
∴四边形ADEO为平行四边形,
∵AD=2$\sqrt{3}$,DE=2,
∴OE=2$\sqrt{3}$,即OF=EF=$\sqrt{3}$,
在Rt△DEF中,根据勾股定理得:DF=$\sqrt{4-3}$=1,即DC=2,
则S菱形ODEC=$\frac{1}{2}$OE•DC=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$.
故答案是:2$\sqrt{3}$.
点评 此题考查了矩形的性质,菱形的判定与性质,以及勾股定理,熟练掌握矩形的性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
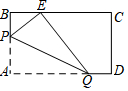 如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.
如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
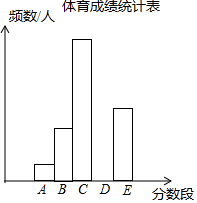 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com