
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
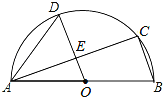
【答案】(1)∠CAD的度数为36°;(2)DE的长为4.
【解析】试题分析:(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
试题解析:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°-∠B=90°-70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=![]() =55°
=55°
∴∠CAD=∠DAO-∠CAB=55°-20°=35°;
(2)在直角△ABC中,BC=![]() .
.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=![]() BC=
BC=![]() .
.
又∵OD=![]() AB=6.5,
AB=6.5,
∴DE=OD-OE=6.5-![]() =4.
=4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
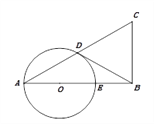
(1)求证: ![]() ;
;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD. 
(1)图中除直角外,请写出一对相等的角吗:(写出符合的一对即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度数.(所求的角均小于平角)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com