
分析 (1)设语言类节目安排x分钟,则器乐类安排x分钟,则歌舞类所用时间为90-2x分钟,根据歌舞类所用时间不少于其余两类节目所用时间总和,列出不等式求解即可;
(3)求得原来每人的捐款数量为(90×100-3000)÷10=600,则后来的人数为10(1+a%),捐款数为(600-600×$\frac{10}{9}$a%),由此列出方程求得答案即可.
解答 解:(1)设语言类节目安排x分钟,则器乐类安排x分钟,则歌舞类所用时间为90-2x分钟,由题意得
90-2x≥x+x
解得:x≤22.5
答:导演组最多给语言类节目安排22.5分钟.
(2)原来每人的捐款数量为(90×100-3000)÷10=600,则后来的人数为10(1+a%),捐款数为(600-600×$\frac{10}{9}$a%),由题意得
(600-600×$\frac{10}{9}$a%)×10(1+a%)=6000
解得:a1=10,a2=0(不合题意,舍去),
答:a的值是10.
点评 此题考查一元二次方程的实际运用,一元一次不等式的实际运用,理解题意,找出题目蕴含的数量关系和不等关系是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
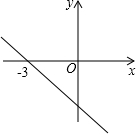 一次函数与方程、不等式的关系
一次函数与方程、不等式的关系查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
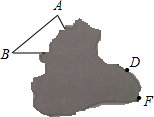 平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.
平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com