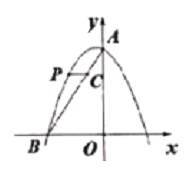
【题目】如图，二次函数y=-x2+(n-1)x+3的图像与y轴交于点A，与x轴的负半轴交于点B(-2，0)
(1)求二次函数的解析式；
(2)点P是这个二次函数图像在第二象限内的一线，过点P作y轴的垂线与线段AB交于点C，求线段PC长度的最大值．
【答案】（1）
；（2）
【解析】
（1）将点B坐标代入即可求出解析式；
（2）先求出直线AB的解析式为
，设点P的坐标为（x，
），则点C的坐标为（
， ），列出线段PC的关系式配方即可得到PC的最大值.
（1）将点B（-2,0）代入y=-x2+(n-1)x+3中，得-4-2（n-1）+3=0，
解得n=
，
∴；
（2）当x=0时得y=3，
∴A（0,3），
设直线AB的解析式为y=kx+b，
，解得
，
∴直线AB的解析式为，
设点P的坐标为（x，），由题意可知点C的纵坐标是，代入，则可得点C的坐标为（， ），
因为C在P的右侧，
∴PC=
=
，
因为点P是这个二次函数图像在第二象限内的一点，所以
，
∴当
时，PC长度的最大值是.
科目：初中数学 来源： 题型：
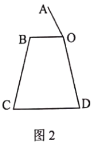
【题目】电水壶采用的是蒸汽智能感应控温原理，具有沸腾后自动断电、防干烧断电的功能．如图1，是一电水壶的实物图．当壶盖打开时，壶盖与闭合时盖面之间的夹角可以抽象为
（如图2），壶身侧面与底座（壶盖及底座厚度护理不计）之间的夹角可以抽象为
（如图2）若壶嘴及手柄部分不考虑，量得壶盖和底座的直径分别为
，
，
．
（1）求底座周长比壶盖周长长多少？（结果保留
）
（2）若量得
，求壶盖最高点到底座所在平面的距离．
（结果精确到
，参考数据：
，
，
，
．）
查看答案和解析>>
科目：初中数学 来源： 题型：
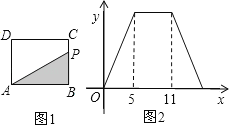
【题目】如图1，在矩形ABCD中，动点P从点B出发，沿BC﹣CD﹣DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，若y关于x的函数图象如图2所示，则y的最大值是（ ）
A.55B.30C.16D.15
查看答案和解析>>
科目：初中数学 来源： 题型：
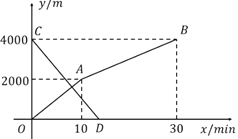
【题目】小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30
．小东骑自行车以300
的速度直接回家，两人距家的路程
与各自离开出发地的时间
之间的函数图像如图所示．
（1）家与图书馆之间的路程为__________
，小玲步行的速度为__________；
（2）求小东距家的路程
关于
的函数表达式；
（3）求两人出发后多长时间相遇．
查看答案和解析>>
科目：初中数学 来源： 题型：
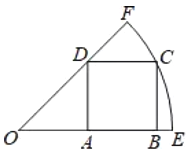
【题目】如图，正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和弧EF上，且点A是线段OB的中点，若弧EF的长为
π，则OD长为______________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（
是常数）的图象与
轴交于
两点（点
在点
的左边）.
（1）如果二次函数的图象经过原点．
①求
的值；
②若
，点
是一次函数
图象上的一点，且
，求
的取值范围；
（2）当
时，函数的最大值为5，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
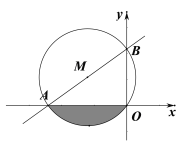
【题目】一次函数
的图像与x轴的负半轴相交于点A，与y轴的正半轴相交于点B，且
△OAB的外接圆的圆心M的横坐标为-3.
（1）求一次函数的解析式；
（2）求图中阴影部分的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为测量底面为圆形的古塔的高度，小红和小明应用不同方法对其展开了研究，以下是他们各自的研究方法和研究数据：
小红：如图1，测角仪
，
的高度均为
，分别测得古塔顶端的仰角为
，
，测角仪底端的距离
为
．
小明：如图2，测角仪
的高度为，测得古塔顶端的仰角为
，测角仪所在位置与古塔底部边缘的最短距离
为
．（参考数据：
，
，
，
，
，
，
）小明利用测得的数据计算古塔高度
．
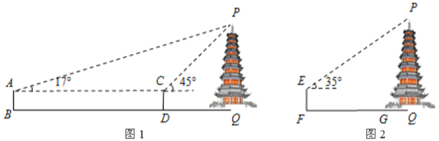
问题1：指出小明计算过程中的错误之处；
问题2：利用两人的测量数据，求出古塔底面圆的半径
（结果精确到
）．
查看答案和解析>>
科目：初中数学 来源： 题型：
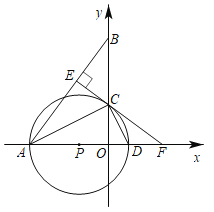
【题目】如图，△AOB中，A（-8，0），B（0，
），AC平分∠OAB，交y轴于点C，点P是x轴上一点，⊙P经过点A、C，与x轴交于点D，过点C作CE⊥AB，垂足为E，EC的延长线交x轴于点F．
（1）求证：EF为⊙P的切线；
（2）求⊙P的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com