练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

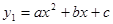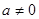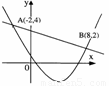
    已知二次函数（）与一次函数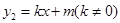的图象相交于点A（－2，4），B（8，2）（如图所示），则能使y1<y2成立的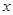的取值范围是　　.

     

    【答案】

    【解析】

    试题分析：直接观察图象即为得到结果.

    由图可知，能使成立的的取值范围是

    考点：本题考查的是图象的交点问题

    点评：解答本题的关键是理解二次函数的图象在一次函数的图象下方的部分满足

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知二次函数y=-
    1
    2
    x2+4x+c的图象经过坐标原点，并且与函数y=
    1
    2
    精英家教网x的图象交于O、A两点．
    （1）求c的值；
    （2）求A点的坐标；
    （3）若一条平行于y轴的直线与线段OA交于点F，与这个二次函数的图象交于点E，求线段EF的最大长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•迎江区一模）已知二次函数的图象经过原点及点（-2，-2），且图象与x轴的另一个交点到原点的距离为4，那么该二次函数的解析式为
    y=
    1
    2
    x2+2x或y=-
    1
    6
    x2+
    2
    3
    x
    y=
    1
    2
    x2+2x或y=-
    1
    6
    x2+
    2
    3
    x
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图，已知二次函数的图像与x轴交于点A、点B（点B在X轴的正半轴上），与y轴交于点C，其顶点为D，直线DC的函数关系式为，又tan∠OBC=1，

    (1） 求a、k的值；（5分）

    (2） 探究：在该二次函数的图像上是否存在点P（点P与点B、C补重合），使得ΔPBC是以BC为一条直角边的直角三角形？若存在，求出点P的坐标，若不存在，请你说明理由（5分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数的图像与x轴交于B（-2，0），C（4，0）两点，点E是对称轴与的交点.

    （1）求二次函数的解析表达式；

    （2）T为对称轴上一动点，以点B为圆心，BT为半径作⊙B，写出直线CT与⊙B相切时，T点的坐标；

    （3）若在x轴上方的P点为抛物线上的动点，且∠BPC为锐角，直接写出PE的取值范围.

    （4）对于（1）中得到的关系式，若为整数，在使得为完全平方数的所有的值中，设的最大值为，最小值为，次小值为，（注：一个数如果是另一个整数的完全平方，那么就称这个数为完全平方数．）求的值．

    y
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数的图像与x轴交于B（-2，0），C（4，0）两点，点E是对称轴与的交点.

    （1）求二次函数的解析表达式；

    （2）T为对称轴上一动点，以点B为圆心，BT为半径作⊙B，写出直线CT与⊙B相切时，T点的坐标；

    （3）若在x轴上方的P点为抛物线上的动点，且∠BPC为锐角，直接写出PE的取值范围.

    （4）对于（1）中得到的关系式，若为整数，在使得为完全平方数的所有的值中，设的最大值为，最小值为，次小值为，（注：一个数如果是另一个整数的完全平方，那么就称这个数为完全平方数．）求的值．

    y
     
     


    查看答案和解析>>

    同步练习册答案