
 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).分析 (1)根据点C(-1,1)确定x轴和y轴,并写出点A的坐标;
(2)画出△A1B1C1,并写出A1、B1、C1的坐标,发现线段BC扫过的图形是一个不规则的图形,由图形可知:△BCO≌△B1C1O,则其面积相等,所以线段BC扫过的面积=扇形OBB1的面积-扇形ODE的面积,利用扇形面积公式代入计算即可.
解答 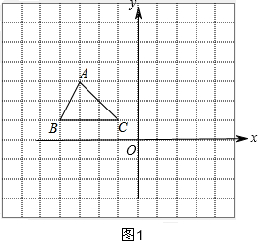 解:(1)如图1,则点A的坐标为(-3,3);
解:(1)如图1,则点A的坐标为(-3,3);
故答案为:(-3,3);
(2)如图2,A1(3,3),B1(1,4),C1(1,1),
∴线段BC扫过的面积=$\frac{90π×(\sqrt{17})^{2}}{360}$-$\frac{90π×(\sqrt{2})^{2}}{360}$=$\frac{15π}{4}$
点评 本题考查了旋转变换和扇形面积的计算问题,同时还利用点的坐标来确定其坐标轴;做好本题要熟知扇形面积的计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S=$\frac{nπ{R}^{2}}{360}$或S=$\frac{1}{2}$lR;对于求某线段扫过的面积或阴影面积问题的主要思路是:将不规则图形面积转化为规则图形的面积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
 有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.
有一块土地形状如图所示,∠B=∠D=90°,AB=5$\sqrt{3}$m,BC=3m,CD=6$\sqrt{2}$m,请计算这块地的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )| A. | 2;SAS | B. | 4;ASA | C. | 2;AAS | D. | 4;SAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm、2cm、3cm、4cm | B. | 3cm、5cm、9cm、15cm | ||
| C. | 2cm、4cm、6cm、8cm | D. | 1cm、3cm、5cm、7cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com