
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
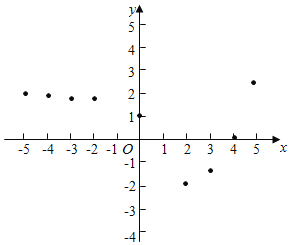
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
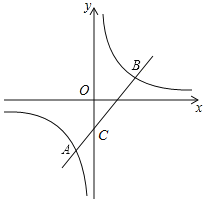
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数y=![]() (k2≠0)的图象交于A(-1,-4)和点B(4,m)
(k2≠0)的图象交于A(-1,-4)和点B(4,m)
(1)求这两个函数的解析式;
(2)已知直线AB交y轴于点C,点P(n,0)在x轴的负半轴上,若△BCP为等腰三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
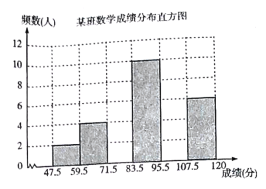
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而增大,正确的是( )
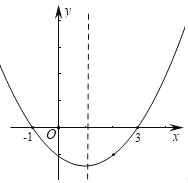
A. ①③B. ②④C. ①②④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=1,且其顶点在直线y=﹣2x﹣2上.
(1)求抛物线的顶点坐标;
(2)求抛物线的解析式;
(3)在给定的平面直角坐标系中画出这个二次函数的图象;
(4)当﹣1<x<4时,直接写出y的取值范围.
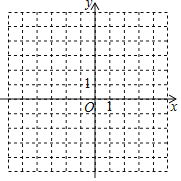
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
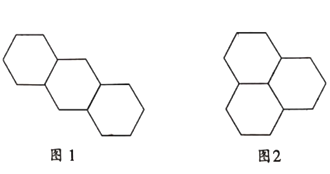
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x(x﹣b)﹣![]() 与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
(1)若点B与点C关于直线x=1对称,求b的值;
(2)若OB=OA,求△BCP的面积;
(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h,求出h与b的关系;若h有最大值或最小值,直接写出这个最大值或最小值.
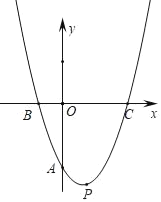
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为圆O的直径,弦AD的延长线与过点C的切线交于点B,E为BC中点,AC= ![]() ,BC=4.
,BC=4.
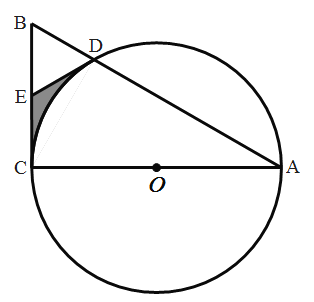
(1)求证:DE为圆O的切线;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
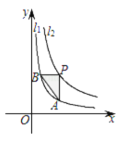
【题目】如图,函数![]() (x>0)和
(x>0)和![]() (x>0)的图象分别是
(x>0)的图象分别是![]() 和
和![]() .设点P在
.设点P在![]() 上,PA∥y轴交
上,PA∥y轴交![]() 于点A,PB∥x轴,交
于点A,PB∥x轴,交![]() 于点B,△PAB的面积为( )
于点B,△PAB的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com