
 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.分析 (1)根据等边三角形的性质得到AB=BC,∠ABC=∠C=60°,再根据三角形全等的判定方法可证得△ABE≌△BCF,则∠BAE=∠FBC,利用三角形外角性质得∠BGE=∠ABG+∠BAE,则∠BGE=∠ABG+∠FBC=∠ABC=60°,然后利用邻补角的定义可计算出∠AGB的度数;
(2)延长GE至点H,使GH=GB,由于∠BGE=60°,根据等边三角形的判定得到△BGH为等边三角形,然后根据等边三角形的性质得到BG=BH=GH,∠GBH=60°,且AB=BD,∠ABD=60°,易得∠ABH=∠DBG,根据三角形全等的判定方法可证得△DBG≌△ABH(SAS),则DG=AH,即可得到DG=AG+BG;
(3)过F作FH∥AE,根据已知条件得到CF:AF=1:2,于是得到BE:EH=3:4,求得BG:GF=3:4,通过△CFH∽△CAE,根据相似三角形的性质得到$\frac{AE}{FH}=\frac{AC}{FC}=3$,$\frac{GE}{FH}=\frac{BG}{BF}=\frac{3}{7}$,于是得到AG:GE=6,即可得到结论.
解答  (1)解:∵△ABC是等边三角形,
(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠C}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°,
∴∠AGB=180°-∠BGE=120°;
(2)证明:延长GE至点H,使GH=GB,如图,
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
在△DBG和△ABH中,
$\left\{\begin{array}{l}{DB=AB}\\{∠DBG=∠ABH}\\{BG=BH}\end{array}\right.$,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG;
(3)过F作FH∥AE,
∵CF=BE,AC=BC,
∵CE=2BE,
∴CF:AF=1:2,
∵FH∥AE,
∴CH:CE=CF:AC=1:3,
∴BE:EH=3:4,
∴BG:GF=3:4,
∵FH∥AE,
∴△CFH∽△CAE,
∴$\frac{AE}{FH}=\frac{AC}{FC}=3$,
∵△BGE∽△BFH,
∴$\frac{GE}{FH}=\frac{BG}{BF}=\frac{3}{7}$,
∴AG:GE=6,
∵BG=3,
∴BF=AE=7,
∴AG=6,
∴DG=BG+AG=9.
点评 本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等边三角形的判定与性质.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
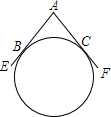 一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.
一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(k>0)上一点,若△AMB是以AB为底的等腰直角三角形,求k的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com