
 小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75) 分析 作AD⊥BC于D,则∠BAD=66°,∠DAC=36°,在Rt△ABD中,求出BD,在Rt△ACD中,求出CD,二者相加即为楼高BC.
解答  解:作AD⊥BC于D,则∠BAD=66°,∠DAC=36°,
解:作AD⊥BC于D,则∠BAD=66°,∠DAC=36°,
在Rt△ACD中,∠ADC=90°,∠CAD=36°,AC=42米,
∴CD=sin36°•AC=0.60×42=25.2(米).
AD=cos36°•AC=0.80×42=33.6(米),
在Rt△ABD中,∠BDA=90°,∠BAD=66°,
∴BD=tan66°•AD=2.25×33.6=75.6(米).
∴BC=BD+CD=75.6+25.2=100.8(米).
答:这栋高楼的高度约为100.8米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,将原三角形转化为两个直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直平分的四边形是矩形 | |
| B. | 邻角相等的菱形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1005 | B. | 1006 | C. | 2012 | D. | 2010 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
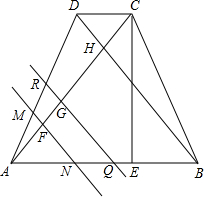 如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3.
如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com