
【题目】如图,已知一次函数y= ![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 ![]() x+b<
x+b< ![]() 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
【答案】
(1)
解:作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求,如图所示.

∵反比例函数y= ![]() (x<0)的图象过点A(﹣1,2),
(x<0)的图象过点A(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数解析式为y=﹣ ![]() (x<0);
(x<0);
∵一次函数y= ![]() x+b的图象过点A(﹣1,2),
x+b的图象过点A(﹣1,2),
∴2=﹣ ![]() +b,解得:b=
+b,解得:b= ![]() ,
,
∴一次函数解析式为y= ![]() x+
x+ ![]() .
.
联立一次函数解析式与反比例函数解析式成方程组: 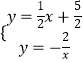 ,
,
解得: 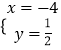 ,或
,或 ![]() ,
,
∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4, ![]() ).
).
∵点A′与点A关于y轴对称,
∴点A′的坐标为(1,2),
设直线A′B的解析式为y=mx+n,
则有  ,解得:
,解得:  ,
,
∴直线A′B的解析式为y= ![]() x+
x+ ![]() .
.
令y= ![]() x+
x+ ![]() 中x=0,则y=
中x=0,则y= ![]() ,
,
∴点C的坐标为(0, ![]() )
)
(2)
解:观察函数图象,发现:
当x<﹣4或﹣1<x<0时,一次函数图象在反比例函数图象下方,
∴当 ![]() x+
x+ ![]() <﹣
<﹣ ![]() 时,x的取值范围为x<﹣4或﹣1<x<0
时,x的取值范围为x<﹣4或﹣1<x<0
【解析】(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求.由点A为一次函数与反比例函数的交点,利用待定系数法和反比例函数图象点的坐标特征即可求出一次函数与反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点A、B的坐标,再根据点A′与点A关于y轴对称,求出点A′的坐标,设出直线A′B的解析式为y=mx+n,结合点的坐标利用待定系数法即可求出直线A′B的解析式,令直线A′B解析式中x为0,求出y的值,即可得出结论;(2)根据两函数图象的上下关系结合点A、B的坐标,即可得出不等式的解集.


科目:初中数学 来源: 题型:
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F. 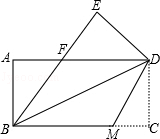
(1)求证:△ABF≌△EDF;
(2)若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料: 2017年1月28日至2月1日农历正月初一至初五,平谷区政府在占地面积6万平方米的琴湖公园举办主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会.
本次庙会共设置了文艺展演区、非遗展示互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区.展区总面积1720平方米.文艺展演区占地面积600平方米,占展区总面积的34.9%;非遗展示区占地190平方米,占展区总面积的11.0%;特色商品区占地面积是文艺展演区的一半,占展区总面积的17.4%;特色美食区占地200平方米,占展区总面积的11.6%;还有孩子们喜爱的儿童娱乐游艺区.
此次庙会本着弘扬、挖掘、展示平谷春节及民俗文化,以京津冀不同地域的特色文化为出发点,全面展示平谷风土人情及津冀人文特色.大年初一,来自全国各地的约3.2万人踏着新春的脚步,揭开了首届平谷庙会的帷幕.大年初二尽管天气寒冷,市民逛庙会热情不减,又约有4.3万人次参观了庙会,品尝特色美食,观看绿都古韵、秧歌表演、天桥绝活,一路猜灯谜、赏图片展,场面火爆.琳琅满目的泥塑、木版画、剪纸、年画等民俗作品也让游客爱不释手,纷纷购买.大年初三,单日接待游客约4万人次,大年初四风和日丽的天气让庙会进入游园高峰,单日接待量较前日增长了约50%.大年初五,活动进入尾声,但庙会现场仍然人头攒动,仍约有5.5万人次来园参观.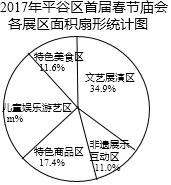
(1)直接写出扇形统计图中m的值;
(2)初四这天,庙会接待游客量约万人次;
(3)请用统计图或统计表,将庙会期间每日接待游客的人数表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.我市区机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题:

(1)A组的频数是 ,本次调查样本的容量是 ;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
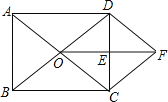
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对![]() ,
, ![]() 定义一种新运算
定义一种新运算![]() ,规定
,规定![]() (其中
(其中![]() ,
, ![]() 均为非零常数),这里等式右边是通常的四则运算,例:
均为非零常数),这里等式右边是通常的四则运算,例: ![]() .
.
已知![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)若关于m的不等式组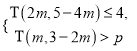 恰好有3个整数解,求实数
恰好有3个整数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B 
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求 ![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红同学在做作业时,遇到这样一道几何题:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点.
(1)依据题意,补全图形;
(2)求∠CEH的度数.
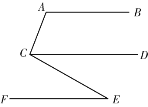
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:

请问小丽的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
x | 1 | 2 | 3 | 4 | 12 | |
y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
请你根据表格回答下列问题:
①这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
②请你写出这个函数的解析式;
③表格中空缺的数值可能是多少?请你给出合理的数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com