Question

15．如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．
（1）若点M的坐标为（3，4），
①求A，B两点的坐标；
②求ME的长．
（2）若$\frac{OK}{MK}$=3，求∠OBA的度数．
（3）设tan∠OBA=x（0＜x＜1），$\frac{OK}{MK}$=y，直接写出y关于x的函数解析式．

Answer 1

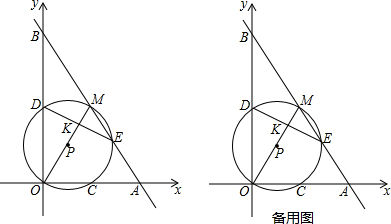
分析 （1）①连接DM、MC，如图1，易证四边形OCMD是矩形，从而得到MD∥OA，MC∥OB，由点M是AB的中点即可得到BD=DO，AC=OC，然后利用点M的坐标就可解决问题；
②根据勾股定理可求出AB的长，从而得到BM的长，要求ME的长，只需求BE的长，只需证△OBM∽△EBD，然后运用相似三角形的性质即可；
（2）连接DP、PE，如图2，由$\frac{OK}{MK}$=3可得OK=3MK，进而得到OM=4MK，PM=2MK，PK=MK．易证△DPK≌△EMK，则有DK=EK．由PD=PE可得PK⊥DE，从而可得cos∠DPK=$\frac{PK}{PD}$=$\frac{1}{2}$，则有∠DPK=60°，根据圆周角定理可得∠DOM=30°．由∠AOB=90°，AM=BM可得OM=BM，即可得到∠OBA=∠DOM=30°；
（3）连接PD、OE，如图3，设MK=t，则有OK=yt，OM=（y+1）t，BM=OM=（y+1）t，DP=PM=$\frac{（y+1）t}{2}$，PK=$\frac{（y-1）t}{2}$．由DP∥BM可得△DKP∽△EKM，则有$\frac{DP}{ME}$=$\frac{PK}{MK}$，由此可得ME=$\frac{y+1}{y-1}$t，从而可求得OE=$\frac{（y+1）t}{y-1}$•$\sqrt{{y}^{2}-2y}$，BE=$\frac{（y+1）yt}{y-1}$，则有x=tan∠OBA=$\frac{OE}{BE}$=$\frac{\sqrt{{y}^{2}-2y}}{y}$，即x²=$\frac{{y}^{2}-2y}{{y}^{2}}$=1-$\frac{2}{y}$，整理得y=$\frac{2}{1-{x}^{2}}$．

解答 解：（1）①连接DM、MC，如图1．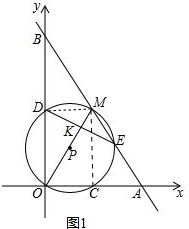
∵OM是⊙P的直径，
∴∠MDO=∠MCO=90°．
∵∠AOB=90°，
∴四边形OCMD是矩形，
∴MD∥OA，MC∥OB，
∴$\frac{BD}{DO}$=$\frac{BM}{AM}$，$\frac{AC}{OC}$=$\frac{AM}{BM}$．
∵点M是AB的中点，即BM=AM，
∴BD=DO，AC=OC．
∵点M的坐标为（3，4），
∴OB=2OD=8，OA=2OC=6，
∴点B的坐标为（0，8），点A的坐标为（6，0）；
②在Rt△AOB中，OA=6，OB=8，
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=10．
∴BM=$\frac{1}{2}$AB=5．
∵∠OBM=∠EBD，∠BOM=∠BED，
∴△OBM∽△EBD，
∴$\frac{BM}{BD}$=$\frac{BO}{BE}$，
∴$\frac{5}{4}$=$\frac{8}{BE}$，
∴BE=$\frac{32}{5}$，
∴ME=BE-BM=$\frac{32}{5}$-5=$\frac{7}{5}$；

（2）连接DP、PE，如图2．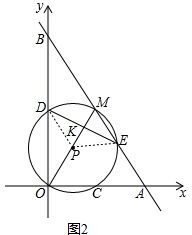
∵$\frac{OK}{MK}$=3，
∴OK=3MK，
∴OM=4MK，PM=2MK，
∴PK=MK．
∵OD=BD，OP=MP，
∴DP∥BM，
∴∠PDK=∠MEK，∠DPK=∠EMK．
在△DPK和△EMK中，
$\left\{\begin{array}{l}{∠PDK=∠MEK}\\{∠DPK=∠EMK}\\{PK=MK}\end{array}\right.$，
∴△DPK≌△EMK，
∴DK=EK．
∵PD=PE，
∴PK⊥DE，
∴cos∠DPK=$\frac{PK}{PD}$=$\frac{1}{2}$，
∴∠DPK=60°，
∴∠DOM=30°．
∵∠AOB=90°，AM=BM，
∴OM=BM，
∴∠OBA=∠DOM=30°；

（3）y关于x的函数解析式为y=$\frac{2}{1-{x}^{2}}$．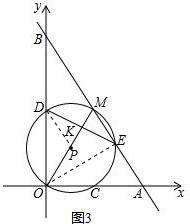
提示：连接PD、OE，如图3．
设MK=t，则有OK=yt，OM=（y+1）t，
BM=OM=（y+1）t，DP=PM=$\frac{（y+1）t}{2}$，
PK=$\frac{（y+1）t}{2}$-t=$\frac{（y-1）t}{2}$．
由DP∥BM可得△DKP∽△EKM，
则有$\frac{DP}{ME}$=$\frac{PK}{MK}$，可得ME=$\frac{y+1}{y-1}$t．
∵OM是⊙P的直径，
∴∠OEM=90°，
∴OE²=OM²-ME²=[（y+1）t]²-[$\frac{y+1}{y-1}$t]²=$\frac{（y+1）^{2}{t}^{2}}{（y-1）^{2}}$•（y²-2y），
即OE=$\frac{（y+1）t}{y-1}$•$\sqrt{{y}^{2}-2y}$，
BE=BM+ME=（y+1）t+$\frac{y+1}{y-1}$t=$\frac{（y+1）yt}{y-1}$，
∴x=tan∠OBA=$\frac{OE}{BE}$=$\frac{\sqrt{{y}^{2}-2y}}{y}$，
∴x²=$\frac{{y}^{2}-2y}{{y}^{2}}$=1-$\frac{2}{y}$，
整理得：y=$\frac{2}{1-{x}^{2}}$．

点评 本题主要考查了圆周角定理、相似三角形的判定与性质、全等三角形的判定与性质、矩形的判定与性质、平行线分线段成比例、三角形中位线定理、直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、勾股定理、三角函数的定义、特殊角的三角函数值等知识，综合性比较强，有一定的难度，通过证明△OBM∽△EBD求出BE是解决第（1）②小题的关键，通过证明△DPK≌△EMK得到DK=EK是解决第（2）小题的关键，设MK=t，然后运用相似三角形的性质、勾股定理求出OE、BE（用y、t的代数式表示）是解决第（3）小题的关键．