练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知∠AOB=45°，A1、A2、A3、…在射线OA上，B1、B2、B3、…在射线OB上，且A1B1⊥OA，A2B1⊥OA，…AnBn⊥OA； A2B2⊥OB，…，An+1Bn⊥OB（n=1，2，3，4，5，6…）．若OA1=1，则AnBn的长是（　　）
    A、
    		2n
    B、(
    		2
    )n
    C、2n
    D、2n-1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，直线y=
    1
    2
    x-1与x轴交于点B，与双曲线y=
    k
    x
    （x＞0）交于点A，过点B作x轴的垂线，与双曲线y=
    k
    x
    交于点C，且AB=AC，则k的值为（　　）
    A、2B、3C、4D、6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

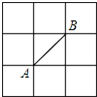    如图的边长为1正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则BC的长不可能是（　　）
    A、
    		2
    B、2
    C、
    		5
    D、
    		10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

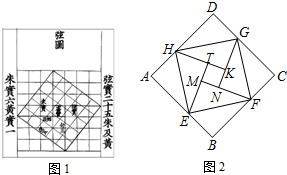    我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图1．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3．若S1+S2+S3=9，则S2的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将直角△ABC绕直角顶点C旋转，使点A落在BC边上的点A′，请你先证明A′B′⊥AB，并利用阴影部分面积完成勾股定理的证明．
    已知：如图，在△ABC中，∠ACB=90°，BC=a，AC=b，AB=c．
    求证：a2+b2=c2．
    证明：作△A′B′C≌△ABC，使点A的对应点A′在边BC上，
    连接AA′、BB′，延长B′A′交AB于点M．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

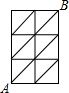    如图，在6个边长为1的小正方形及其部分对角线构成的图形中，如图从A点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有（　　）
    A、1种B、2种C、3种D、4种

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，D，E分别是边AB，AC的中点．若DE=2，则BC=（　　）
    A、2B、3C、4D、5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，四边形ABCD、BEFD、EGHD均为平行四边形，其中C、F两点分别在EF、GH上．若四边形ABCD、BEFD、EGHD的面积分别为a、b、c，则关于a、b、c的大小关系，下列何者正确？（　　）
    A、a＞b＞cB、b＞c＞aC、c＞b＞aD、a=b=c

    查看答案和解析>>

    科目：初中数学 来源： 题型：

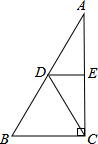    如图，在Rt△ACB中，∠ACB=90°，点D、E分别为边AB、AC的中点，连接CD，且BD=2DE，BC=4，则AC的长为（　　）
    A、4
    		2
    B、4
    		3
    C、8
    D、8
    		3

    查看答案和解析>>

    同步练习册答案