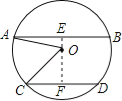
【题目】⊙o的半径是13，弦AB∥CD，AB=24，CD=10，则AB与CD的距离是（ ）
A．7 B．17 C．7或17 D．4
【答案】C.
【解析】
试题分析： ①当AB、CD在圆心两侧时；过O作OE⊥AB交AB于E点，过O作OF⊥CD交CD于F点，连接OA、OC，如图所示：∵半径r=13，弦AB∥CD，且AB=24，CD=10，∴OA=OC=13，AE=EB=12，CF=FD=5，E、F、O在一条直线上，∴EF为AB、CD之间的距离，在Rt△OEA中，由勾股定理可得：OE2=OA2﹣AE2，∴OE=
=5，在Rt△OFC中，由勾股定理可得：OF2=OC2﹣CF2，∴OF=
=12，∴EF=OE+OF=17，AB与CD的距离为17；
②当AB、CD在圆心同侧时；同①可得：OE=5，OF=12；则AB与CD的距离为：OF﹣OE=7；故AB与CD的距离是为7或17．故选C．
科目：初中数学 来源： 题型：
【题目】某班数学学习小组某次测验成绩分别是63，72，70，49，66，81，53，92，69，则这组数据的极差是（ ）
A. 47 B. 43 C. 34 D. 29
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．
⑴若∠BAE=40°，求∠C的度数；
⑵若△ABC周长13cm，AC=6cm，求DC长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，∠BAC=45°，AB=BC.
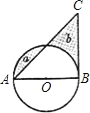
（1）求证：BC是⊙O的切线；
（2）设阴影部分的面积为a，b，⊙O的面积为S，请写出S与a，b的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
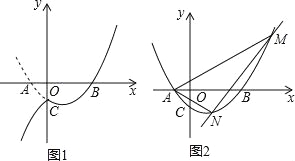
【题目】已知抛物线y=（m﹣1）x2+（m﹣2）x﹣1与x轴交于A、B两点，若m＞1，且点A在点B的左侧，OA：OB=1：3
（1）试确定抛物线的解析式；
（2）直线y=kx﹣3与抛物线交于M、N两点，若△AMN的内心在x轴上，求k的值．
（3）设（2）中抛物线与y轴的交点为C，过点C作直线l∥x轴，将抛物线在y轴左侧的部分沿直线l翻折，抛物线的其余部分保持不变，得到一个新图象，请你结合新图象回答：当直线y=
x+b与新图象只有一个公共点P（x0，y0）且y0≤7时，求b的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在a﹣（2b﹣3c）=﹣□中的□内应填的代数式为（ ）
A. ﹣a﹣2b+3c B. a﹣2b+3c C. ﹣a+2b﹣3c D. a+2b﹣3c
查看答案和解析>>
科目：初中数学 来源： 题型：
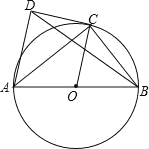
【题目】如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．
（1）求证：AC平分∠DAB；
（2）若sin∠ABC=
，求tan∠BDC的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com