
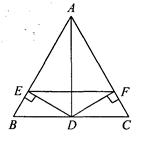
 ,
, ;(2)证明详见解析.
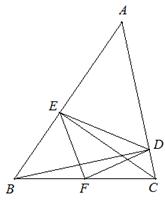
;(2)证明详见解析.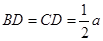 ,利用三线合一得到AD⊥BC,利用勾股定理求出AD的长;由∠B=60°,DE垂直于AB,得到∠EDB=30°,利用30°所对的直角边等于斜边的一半求出
,利用三线合一得到AD⊥BC,利用勾股定理求出AD的长;由∠B=60°,DE垂直于AB,得到∠EDB=30°,利用30°所对的直角边等于斜边的一半求出 ,同理可得
,同理可得 ,所以AE=AF,进而可得等边三角形AEF。而AE=AB-BE,即可求出EF的长。
,所以AE=AF,进而可得等边三角形AEF。而AE=AB-BE,即可求出EF的长。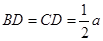
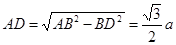
 ,
,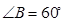
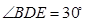
 ,同理可得:
,同理可得:
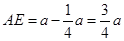



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com