
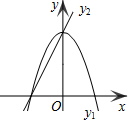
 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 观察图象,当x>0,一次函数图象在二次函数图象的上方,则可对①进行判断;利用一次函数和二次函数的增减性可对②进行判断;利用二次函数的最值和M的意义可对③进行判断;分别解-2x2+2=1和2x+2=1,再计算出对应的M的值,从而可对④进行判断.
解答 解:当x>0时,y1<y2,所以①错误;
当x<0时,y1、y2都随x的增大而增大,则x值越大,M值越大,所以②错误;
因为抛物线y1=-2x2+2有最大值为2,所以y1、y2中的较小值M不可能大于2,所以③正确;
若-2x2+2=1,解得x=±$\frac{\sqrt{2}}{2}$,当x=$\frac{\sqrt{2}}{2}$时,M=1;若2x+2=1,解得x=-$\frac{1}{2}$,此时M=1,所以④正确.
故选B.
点评 本题考查了二次函数与不等式(组):对于二次函数y=ax2+bx+c(a、b、c是常数,a≠0)与不等式的关系,一般要转化成关于x的不等式,解不等式求得自变量x的取值范围.或利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 45000名学生是总体 | |
| B. | 1500名学生的身高是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
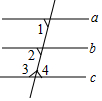 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com