
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠DAC的度数;
(2)四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求△AB′D的面积.

【答案】(1)∠DAC=90°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由于AB=BC=1,且∠B=90°根据勾股定理即可求出AC的长度,而CD=![]() ,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠DAC的度数;
,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠DAC的度数;
(2)首先把求四边形ABCD的面积分割为求△ABC和△ACD的面积,然后利用三角形的面积公式可以分别求出这两个三角形的面积,最后就可以求出四边形ABCD的面积;
(3)作出△AB′D的边AB′边上的高DE,证明△ADE为等腰直角三角形,从而利用勾股定理可求出DE的长,进一步可得出△AB′D的面积.
解:(1)∵AB=BC=1,∠B=90°,
∴∠BAC=∠ACB=45°,AC=![]() =
=![]() .
.
又∵CD=![]() ,DA=1,
,DA=1,
∴AC2+DA2=CD2.
∴△ADC为直角三角形,∠DAC=90°.
(2)∵S△ABC=![]() AB·BC=
AB·BC=![]() ,
,
S△ADC=![]() AD·AC=
AD·AC=![]() ,
,
∴S四边形ABCD=S△ABC+S△ADC=![]() .
.
(3)过点D作DE⊥AB′,垂足为E,
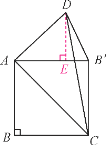
由(1)知∠DAC=90°.
根据折叠可知∠B′AC=∠BAC=45°,AB=AB′=1,S△AB′C=S△ABC=![]() .
.
∴∠DAE=∠DAC-∠B′AC=45°,∴∠DAE=∠AED=45°,
∴AE=DE.
在Rt△ADE中,AE2+DE2=AD2,
∴2DE2=1.∴DE=![]() .
.
∴S△ADB′=![]() ×AB′×DE=
×AB′×DE=![]() ×1×
×1×![]() =
=![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
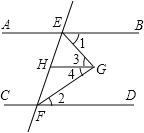
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3
又∵HG∥CD(已知)
∴∠2=∠4
∵AB∥CD(已知)
∴∠BEF+ =180°
又∵EG平分∠BEF(已知)
∴∠1=![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2=![]() ∠
∠
∴∠1+∠2=![]() ( )
( )
∴∠1+∠2=90°
∴∠3+∠4=90° 即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.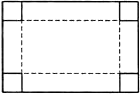
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() 将直线
将直线![]() 向上平移
向上平移![]() 个单位得直线
个单位得直线![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() 且点
且点![]() 的横坐标为
的横坐标为![]()

(1)求直线![]() 的解析式;
的解析式;
(2)连接![]() 求
求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,正方形如图摆放,已知顶点 A(a,0),B(0,b) ,则顶点C的坐标为( )
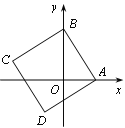
A.(-b,a b)B.(-b,b - a)C.(-a,b - a)D.(b,b -a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述何者正确( )
A.O是△AEB的外心,O是△AED的外心
B.O是△AEB的外心,O不是△AED的外心
C.O不是△AEB的外心,O是△AED的外心
D.O不是△AEB的外心,O不是△AED的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
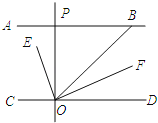
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有_____填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com