
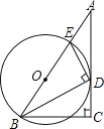
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,DE⊥BD交AB于点E,设⊙O是△BDE的外接圆.
(1)求证:AC是⊙O的切线;
(2)探究线段BC,BD,BO之间的数量关系,并证明;
(3)若DC=2,BC=4,求AD的长.
【答案】(1)见解析;(2)BD2=2BOBC,理由见解析;(3)![]()
【解析】
(1)连接OD,由半径相等得到∠OBD=∠ODB,再由BD为角平分线,得到∠OBD=∠CBD,从而证得∠ODB =∠CBD,OD∥BC,得到∠ODC=90°,即可得证;
(2)BD2=2BOBC,理由为:由三角形EBD与三角形DBC相似,得比例式,将BE换为2BO即可得证;
(3)在直角三角形DBC中,利用勾股定理求出BD的长,根据(2)的关系式求出BO的长,即为OD的长,由OD与BC都与AC垂直,得到OD与BC平行,由平行得比例,即可求出AD的长.
(1)证明:连接OD,
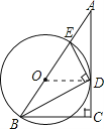
∵OB=OD,
∴∠OBD=∠ODB,
∵BD为角平分线,
∴∠OBD=∠CBD,
∴∠ODB =∠CBD,
∴OD∥BC,
∵∠C=90°,
∴∠ODC=90°,
则AC为圆O的切线;
(2)BD2=2BO![]() BC,
BC,
理由为:
∵∠C=∠BDE=90°,∠ABD=∠DBC,
∴△EBD∽△DBC,
∴![]() =
=![]() ,即DB2=EBBC,
,即DB2=EBBC,
∵EB=2BO,
∴BD2=2BO![]() BC;
BC;
(3)在Rt△BDC中,BC=4,DC=2,
根据勾股定理得:BD=![]() =2
=2![]() ,
,
∴由BD2=2BO![]() BC,得BO=OD=
BC,得BO=OD=![]() =
=![]() ,
,
∵OD∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:AD=![]() .
.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著在数学上有其独到的成就,不仅最早提到了分数问题,首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱又会缺16文钱,问买鸡的人数、鸡的价格各是多少?通过计算可得买鸡的人数是( )
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为_____.
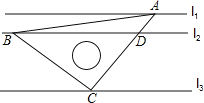
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,5)且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:①a﹣b+c>0;②2a+b=0;③b2﹣4ac>0;④一元二次方程ax2+bx+c=5有两个不相等的实数根.其中正确结论的个数是( )
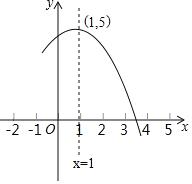
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com