
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的⊙O过点E. 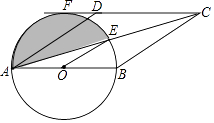
(1)求证:四边形ABCD的是菱形;
(2)若CD的延长线与圆相切于点F,已知直径AB=4,求阴影部分的面积.
【答案】
(1)证明:
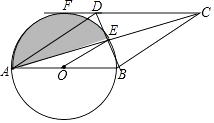
∵AE=CE,BE=ED,
∴四边形ABCD是平行四边形,
∵AB为直径,
∴∠AEB=90°,
即AC⊥BD,
∴四边形ABCD是菱形
(2)解:连接OF,
∵CF为⊙O的切线,
∴∠OFC=90°,
∵AB=4,
∴OA=OB=2,
∵四边形ABCD是菱形,
∴AB=AD=4,
过D作DH⊥AB于H,
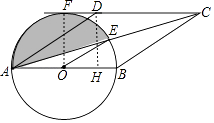
则DH=OF=2,
∠DAH=30°,
∵四边形ABCD是菱形,
∴∠DAC=∠BAC=15°,
∴∠BOE=2∠BAC=30°,
∴S扇形BOE= ![]() =
= ![]() ,S△AOE=
,S△AOE= ![]() =1,
=1,
∴S阴影=S半圆O﹣S△AOE﹣S扇形BOE= ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() π﹣1
π﹣1
【解析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,再根据菱形的判定得出即可;(2)连接OF,过D作DH⊥AB于H,分别求出扇形BOE、△AOE、半圆O的面积,即可得出答案.


科目:初中数学 来源: 题型:
【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
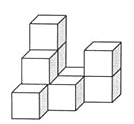
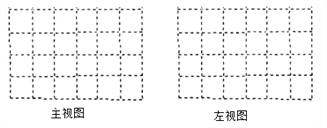
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
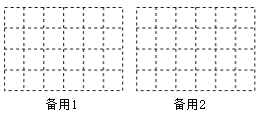
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE//BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
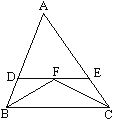
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若一次函数![]() 的图象与x轴的交于点
的图象与x轴的交于点![]() ,与y轴交于点
,与y轴交于点![]() 下列结论:①关于x的方程
下列结论:①关于x的方程![]() 的解为
的解为![]() ;②
;②![]() 随x的增大而减小;③关于x的方程
随x的增大而减小;③关于x的方程![]() 的解为
的解为![]() ;④关于x的不等式
;④关于x的不等式![]() 的解为
的解为![]() 其中所有正确的为
其中所有正确的为![]()
![]()

A. ①②③ B. ①③ C. ①②④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别是边BC,AC的中点,AD与BE相交于点
中,点D,E分别是边BC,AC的中点,AD与BE相交于点![]() 点F,G分别是线段AO,
点F,G分别是线段AO,
BO的中点.
![]() 求证:四边形DEFG是平行四边形;
求证:四边形DEFG是平行四边形;
![]() 如图2,连接CO,若
如图2,连接CO,若![]() ,求证:四边形DEFG是菱形;
,求证:四边形DEFG是菱形;
![]() 在
在![]() 的前提下,当
的前提下,当![]() 满足什么条件时,四边形DEFG能成为正方形?
满足什么条件时,四边形DEFG能成为正方形?![]() 直接回答即可,不必证明
直接回答即可,不必证明![]()
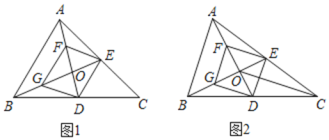
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为线段AD外一点,M、C、B、N为AD上任意四点,连接OM、OC、OB、ON,下列结论不正确的是( )
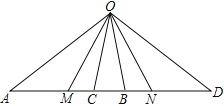
A. 以O为顶点的角共有15个
B. 若OM平分∠AOC,ON平分∠BOD,∠AOD=5∠COB,则∠MON=![]() (∠MOC+∠BON)
(∠MOC+∠BON)
C. 若M为AB中点,N为CD中点,则MN=![]() (AD-CB)
(AD-CB)
D. 若MC=CB,MN=ND,则CD=2CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.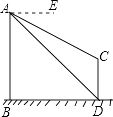
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com