练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知两相似三角形对应高之比是1：2，则它们的面积之比为1：4．

    分析 根据相似三角形的对应高的比的比等于相似比求出相似比，根据面积的比等于相似比的平方解答．

    解答 解：∵两相似三角形对应高之比是1：2，
    ∴两相似三角形相似比是1：2，
    ∴这两相似三角形面积比是1：4，
    故答案为：1：4．

    点评 本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．点P与点Q位于线段MN的两侧，
    （1）如图甲，若△PMN和△QMN中，PI平分外角∠SPN，并与线段MN的延长线交于点I，连接QI，若△PMN≌△QMN，求证：QI平分外角∠TQN；
    （2）如图乙，若△PMN和△QMN中，PM+PN=QM+QN，且外角∠SPN和∠TQN的角平分线PI、QI相交于点I，连接MI，求证：MI平分∠PMQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．有六张卡片，上面各写有1，1，2，3，4，4六个数，从中任意摸一张，摸到奇数的概率是（　　）
    A．$\frac{1}{6}$B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图所示，直线y=x+2与x轴交于点A，与y轴交于点B，AB⊥BC，且点C在x轴上，若抛物线y=ax2+bx+c以C为顶点，且经过点B，求这条抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知抛物线y=$\frac{1}{2}$x2+x+m与x轴交于A，B两点，与y轴交于点C．
    （1）求m的取值范围；
    （2）当AB=4时，在该抛物线上是否存在点P，使得△ABP的面积是△ABC的面积的2倍？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列事件中，属于不确定事件的是（　　）
    A．成都市的人口比广汉市的人口多
    B．从装有50个黄球的袋中随机取出2个球，都是白球
    C．每晚7点，中央电视台1套播出“新闻联播”节目
    D．从装有10个黄球、4个白球的袋中，随机取出两个球，一个黄球，一个白球

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

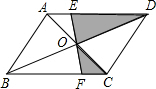    6．如图，?ABCD的面积是8，对角线AC、DB交于点O，EF过点O分别交AD、BC于E、F，则阴影部分的面积是（　　）
    A．4B．2C．6D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）过坐标系的原点O，与x轴的另一个交点为B，顶点坐标为A（$\sqrt{3}$，1）．
    （1）求：a、b、c的值；
    （2）将△OAB绕原点O顺时针旋转120°，旋转后的三角形设为△OA′B′（点A′对应点A，点B′对应点B），试判断点B′是否在抛物线y=ax2+bx+c（a≠0）上；
    （3）设点P是抛物线y=ax2+bx+c（a≠0）上的一点，且PA=PA′，写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列式子从左到右的变形中，属于因式分解的是（　　）
    A．（x+1）（x-1）=x2-1B．a2-b2=（a+b）（a-b）
    C．x2-2x+1=x（x-2）+1D．mx+my+nx+ny=m（x+y）+n（x+y）

    查看答案和解析>>

    同步练习册答案