
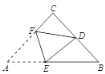
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则cos∠BED的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=∠CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理可求出CF的值.在Rt△FCD中,根据余弦的定义即可得出结论.
∵△DEF是△AEF翻折而成,∴△DEF≌△AEF,∠A=∠EDF.
∵△ABC是等腰直角三角形,∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,∴∠BED=∠CDF.
设CD=1,CF=x,则CA=CB=2,∴DF=FA=2﹣x.
在Rt△CDF中,由勾股定理得:CF2+CD2=DF2,即x2+1=(2﹣x)2,解得:x![]() ,DF= 2﹣x=
,DF= 2﹣x=![]() =
=![]() ,∴cos∠BED=cos∠CDF
,∴cos∠BED=cos∠CDF![]() .
.
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点An的坐标为__.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点An的坐标为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魏晋时期的数学家刘徽首创割圆术.为计算圆周率建立了严密的理论和完善的算法.作圆内接正多边形,当正多边形的边数不断增加时,其周长就无限接近圆的周长,进而可用![]() 来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
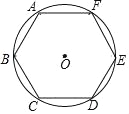
A. 0.5B. 1C. 3D. π
查看答案和解析>>
科目:初中数学 来源: 题型:
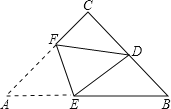
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,B、D 分别是 x 轴和 y 轴的正半轴上的点,AD∥x 轴,AB∥y 轴(AD>AB),点 P 从 C 点出发,以 3cm/s 的速度沿 CDAB 匀速运动,运动到 B 点时终止;点 Q 从 B 点出发,以 2cm/s 的速度,沿 BCD 匀速运动,运动到 D 点时终止.P、Q 两点同时出发, 设运动的时间为 t(s),△PCQ 的面积为 S(cm2),S 与 t 之间的函数关系由图 2 中的曲线段 OE,线段 EF、FG 表示.
(1)求 AD 点的坐标;
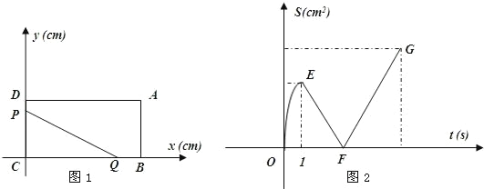
(2)求图2中线段FG的函数关系式;
(3)是否存在这样的时间 t,使得△PCQ 为等腰三角形?若存在,直接写出 t 的值;若不存在, 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学公司组织初三505名学生外出社会综合实践活动,现打算租用A、B 两种型号的汽车,并且每辆车上都安排1名导游,如果租用这两种型号的汽车各5辆,则刚好坐满;如果全部租用B型汽车,则需13辆汽车,且其中一辆会有2个空位,其余汽车都坐满.(注:同种型号的汽车乘客座位数相同)
(1)A、B两种型号的汽车分别有多少个乘客座位?
(2)综合考虑多种因素,最后该公司决定租用9辆汽车,问最多安排几辆B型汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数y=﹣2x+5,下列表述:
①图象一定经过(2,﹣1);②图象经过一、二、四象限;③与坐标轴围成的三角形面积为12.5;④x每增加1,y的值减少2;⑤该图象向左平移1个单位后的函数表达式是y=﹣2x+4,正确的是( )
A. ①③B. ②⑤C. ②④D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
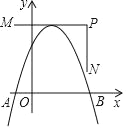
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com