
【题目】如图所示,△ABC中,D是BC中点,E是AD中点,过点A作BC的平行线交CE的延长线于F,连接BF.
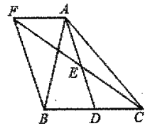
(1)判断并证明四边形AFBD的形状;
(2)当ΔABC满足什么条件时,四边形AFBD是矩形,证明你的结论.
【答案】(1)见解析 (2)见解析
【解析】
(1)由于E是AD中点,则AE=DE,而AF∥BC,那么∠FAE=∠CDE,又∠AEF=∠DEC,利用ASA可证△AFE≌△DCE,于是有AF=CD,又AD是中线,则BD=CD,等量代换有AF=BD;
(2)结论:AB=AC.由(1)知四边形AFBD是平行四边形,而AB=AC,AD是中线,利用等腰三角形三线合一定理,可证AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
解:(1)四边形AFBD是平行四边形.
理由如下:∵点E是AD的中点,
∴AE=DE,
又∵AF∥BD,
∴∠FAE=∠CDE,
又∵∠FEA=∠CED,
∴△AFE≌△DCE(ASA),
∴AF=CD,
又∵AD是BC边上的中线,
∴BD=CD,
∴AF=BD,
∵AF∥BD,
∴四边形AFBD是平行四边形.
(2)当AB=AC时,四边形AFBD是矩形.
理由如下:
∵AB=AC,BD=CD,
∴AD⊥BC,
∴∠ADB=90°,
∵四边形AFBD为平行四边形,
∴四边形AFBD为矩形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③![]() =
=![]() ;④AD·BC=DE·AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
;④AD·BC=DE·AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )

A.1个B.2C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某城建部门计划在新修的城市广场的一块长方形空地上修建一个面积为1200m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为50m,宽为40m.

(1)求通道的宽度;
(2)某公司希望用80万元的承包金额承揽修建广场的工程,城建部门认为金额太高需要降价,通过两次协商,最终以51.2万元达成一致,若两次降价的百分率相同,求每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个函数图象上每个点的纵坐标变为原来的倒数(原函数图象上纵坐标为0的点除外)横坐标不变,可以得到另一个函数的图象,我们称这个过程为倒数变换.
例如:如图1,将y=x的图象经过倒数变换后可得到y=![]() 的图象.特别地,因为y=x图象上纵坐标为0的点是原点,所以该点不作变换,因此y=
的图象.特别地,因为y=x图象上纵坐标为0的点是原点,所以该点不作变换,因此y=![]() 的图象上也没有纵坐标为0的点.
的图象上也没有纵坐标为0的点.
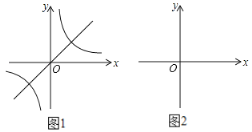
(1)请在图2中画出y=﹣x﹣1的图象和它经过倒数变换后的图象;
(2)观察上述图象,结合学过的关于函数图象和性质的知识.
①猜想:倒数变换得到的图象和原函数的图象之间可能有怎样的联系?写出两条即可.
②说理:请简要解释你其中一个猜想;
(3)设图2中的图象的交点为A,B,若点C的坐标为(﹣1,m),△ABC的面积为6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
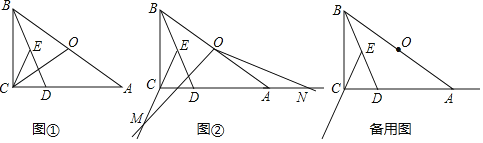
(1)如图①,连接OC,证明∠OCE=∠OAC;
(2)如图②,点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车已知该型号汽车的进价为10万元/辆,经销一段时间后发现:当该型号汽车售价定为20万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆
(1)若每辆汽车的售价降低x万元,则每周的销售量是 辆(用含x的代数式表示)
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,需将每辆汽车的售价降低多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于点B,C,连接AC.
(m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于点B,C,连接AC.
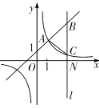
(1)求k和m的值;
(2)求点B的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com