
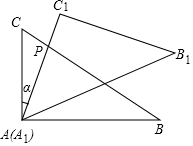
 如图,是一副三角板,在△ABC 中,∠A=90°,∠C=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=AB.若将边A1C1与边AC重合,其中点A1与点A重合.将三角板A1B1C1绕点A(A1)按顺时针方向旋转,旋转角为α,旋转过程中边A1C1与边BC的交点为P,设AC=m.
如图,是一副三角板,在△ABC 中,∠A=90°,∠C=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=AB.若将边A1C1与边AC重合,其中点A1与点A重合.将三角板A1B1C1绕点A(A1)按顺时针方向旋转,旋转角为α,旋转过程中边A1C1与边BC的交点为P,设AC=m.分析 (1)在Rt△ABC中,由特殊锐角三角函数值,先求得AB的长,然后在Rt△A1B1C1中利用特殊锐角三角函数即可求得A1C1的长;
(2)利用三角形的外角的性质求得∠APB=90°,然后利用同位角相等,两直线平行进行判定即可;
(3)如下图:作PH⊥AB于H.求出PH即可解决问题;
(4)根据S重叠部分=${S}_{△AF{C}_{1}}$-${S}_{△PD{C}_{1}}$计算即可解决问题;
解答 解:(1)在Rt△ABC中,∠C=60°,AC=m,
由特殊锐角三角函数可知:$\frac{AB}{AC}$=tan60°=$\sqrt{3}$,
∴AB=$\sqrt{3}$m.
∴AB1=$\sqrt{3}$m
在Rt△A1B1C1,∠B1=∠45°,
∴$\frac{{A}_{1}{C}_{1}}{A{B}_{1}}$=$\frac{\sqrt{2}}{2}$.
∴A1C1=$\frac{\sqrt{2}}{2}$×$\sqrt{3}$m=$\frac{\sqrt{6}}{2}$m.
(2)∵∠CAP=30°,∠C=60°,
∴∠APB=∠C+∠CAP=90°.
∴∠C1=∠APB,.
∴B1C1∥BC.
(3)如下图:作PH⊥AB于H.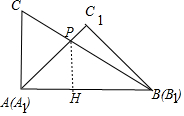
∵∠PAH=45°,
∴可以假设PH=AH=x,则BH=$\sqrt{3}$x,
∴x+$\sqrt{3}$x=$\sqrt{3}$($\sqrt{6}$+$\sqrt{2}$),
解得x=$\sqrt{6}$,
∴S重叠部分=$\frac{1}{2}$•AB•PH=$\frac{1}{2}$•$\sqrt{3}$($\sqrt{6}$+$\sqrt{2}$)•$\sqrt{6}$=3$\sqrt{3}$+3.
(4)如图,设B1C1交AB于F,交BC于D.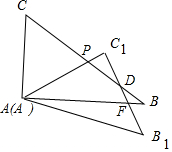
由(1)可知:AC1=$\frac{\sqrt{6}}{2}$m,
在Rt△AFC1中,FC1=$\frac{\sqrt{2}}{2}$m,
∴${S}_{△AF{C}_{1}}$=$\frac{1}{2}$$\frac{\sqrt{2}}{2}$m•$\frac{\sqrt{6}}{2}$m=$\frac{\sqrt{3}}{4}$m2,
由题意△ACP是等边三角形,
∴PC1=$\frac{\sqrt{6}}{2}$m-m,DC1=$\sqrt{3}$($\frac{\sqrt{6}}{2}$m-m),
∴${S}_{△PD{C}_{1}}$=$\frac{1}{2}$•$\sqrt{3}$($\frac{\sqrt{6}}{2}$m-m)2=$\frac{5\sqrt{3}-6\sqrt{2}}{4}$m2,
∴S重叠部分=${S}_{△AF{C}_{1}}$-${S}_{△PD{C}_{1}}$=$\frac{\sqrt{3}}{4}$m2-($\frac{5\sqrt{3}-6\sqrt{2}}{4}$m2)=$\frac{3\sqrt{2}-2\sqrt{3}}{2}$m2.
点评 本题主要考查的是锐角三角函数和三角形的综合应用,难度较大,解答本题的关键是灵活应用锐角函数求得相关线段的长度.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{35}{2}$ | B. | 10 | C. | 8$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
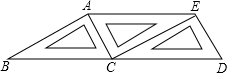 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
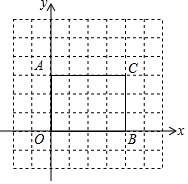 如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).
如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com