
 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
分析 (1)根据D项目的频数及频率可得总数,再依据频率=频数÷总数可得答案;
(2)根据分布表可补全条形图,依据众数、中位数定义可得;
(3)用A、B的频率和乘以总人数可得.
解答 解:(1)本次一共抽取的学生数为5÷0.1=50,
k=50×0.2=10,m=50×0.5=25,n=10÷50=0.2,
故答案为:50,10,25,0.2;
(2)补全频数分布直方图如下: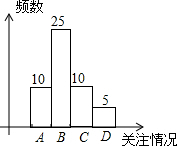
则众数为B:一般关注;
其中位数为第25、26个数据的平均数,由条形图知第25、26个数据均为B:一般关注,
则中位数为B:一般关注;
(3)2000×(0.5+0.2)=1400,
答:估计该校对体育中考改革关注(含高度关注和一般关注)的学生人数约为1400人.
点评 本题考查频数分布直方图、样本、总体、样本容量、用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.
现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
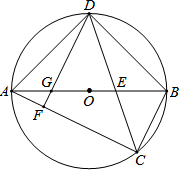 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
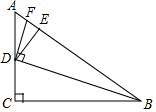 如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将
如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com