
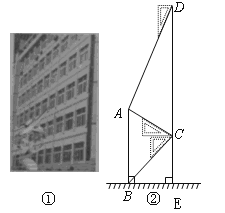
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为![]() ,底部B点的俯角为
,底部B点的俯角为![]() ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为![]() (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() ).
).
【答案】![]()
【解析】试题分析:
由题意可得:∠ADC=30°,∠ACD=60°,∠BCE=45°,∠ABE=∠BEC=90°,由此可得∠DAC=180°-30°-60°=90°,结合CD=10可得AC=5;过点A作AF⊥DE于点F,则∠AFE=90°,从而在△AFC中由∠ACD=60°可得∠CAF=30°,由此可得CF=2.5,AF=![]() ,再证四边形ABEF是矩形可得BE=AF=
,再证四边形ABEF是矩形可得BE=AF=![]() ,结合∠BCE=45°,∠BEC=90°可得CE=BE=
,结合∠BCE=45°,∠BEC=90°可得CE=BE=![]() ,从而可得AB=EF=CF+BE=2.5+
,从而可得AB=EF=CF+BE=2.5+![]() .
.
试题解析:
由题意可得:∠ADC=30°,∠ACD=60°,∠BCE=45°,∠ABE=∠BEC=90°,
∴在△ADC中,∠DAC=180°-30°-60°=90°,
又∵CD=10,∠D=30°,
∴AC=5,
过点AF⊥CD于点F,
∴∠AFC=90°,
∵∠ACD=60°,
∴∠CAF=30°,
∴CF=2.5,AF=AC·sin60°=![]() ,
,
∵∠ABE=∠BEF=∠AFE=90°,
∴四边形ABEF是矩形,
∴BE=AF=![]() ,AB=EF,
,AB=EF,
∵在△BEC中,∠BEC=90°,∠BCE=45°,
∴CE=BE=![]() ,
,
∴AB=EF=CE+CF=2.5+![]()
![]() 6.8.
6.8.



科目:初中数学 来源: 题型:
【题目】列方程式应用题.
天河食品公司收购了200吨新鲜柿子,保质期15天,该公司有两种加工技术,一种是加工为普通柿饼,另一种是加工为特级霜降柿饼,也可以不需加工直接销售.相关信息见表:
品种 | 每天可加工数量(吨) | 每吨获利(元) |
新鲜柿子 | 不需加工 | 1000元 |
普通柿饼 | 16吨 | 5000元 |
特级霜降柿饼 | 8吨 | 8000元 |
由于生产条件的限制,两种加工方式不能同时进行,为此公司研制了两种可行方案:
方案1:尽可能多地生产为特级霜降柿饼,没来得及加工的新鲜柿子,在市场上直接销售;
方案2:先将部分新鲜柿子加工为特级霜降柿饼,再将剩余的新鲜柿子加工为普通柿饼,恰好15天完成.
请问:哪种方案获利更多?获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
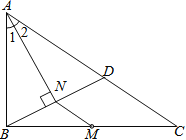
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
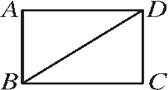
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
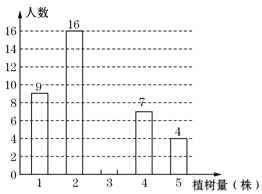
【题目】为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
(1)求该班的总人数、植树株数的众数,并把条形统计图补充完整;
(2)若将该班同学的植树人数所占比例绘制成扇形统计图时,求“植树3株”对应扇形的圆心角的度数;
(3)求从该班参加植树的学生中任意抽取一名,其植树株数超过该班植树株数的平均数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com