
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
①最大的负整数是﹣1;②数轴上表示数2 和﹣2的点到原点的距离相等;③当a≤0时,|a|=﹣a成立;④a的倒数是![]() ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.
A. 2 个 B. 3 个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定一个四边形是平行四边形的是( )
A. 两组对边分别平行B. 一组对边平行且相等C. 两组对角分别相等 D. 一组对边相等且一组对角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙的空地上,用长为24米的篱笆围成中间隔有二道篱笆的长方形花圃,从设计的美观角度出发,墙的最小可用长度为4米,墙的最大可用长度为14米.
(1)若所围成的花圃的面积为32平方米,求花圃的宽AB的长度;
(2)当AB的长为 时,所围成的花圃面积最大,最大值为 米2;当AB的长为 时,所围成的花圃面积最小,最小值为 米2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
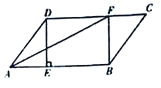
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AD∥BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点且AE:BE=1:2,F为BC一动点,∠FEG=∠B,EG交射线BC于G,直线EG交射线CA于H.
(1)求sin∠ABC;
(2)求∠BAC的度数;
(3)设BF=x,CH=y,求y与x的函数关系式及其定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com