
【题目】近年来,随着新能源汽车推广力度加大,产业快速发展,越来越多的消费者开始接受并购买新能源汽车,我国新能源汽车的生产量和销售量都大幅增长,下图是2014-2017年新能源汽车生产和销售的情况:根据统计图中提供的信息,预估全国2018年新能源汽车销售量约为__________万量,你的预估理由是____________________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 相交于点
相交于点![]() ,
,![]() 分别为
分别为![]() 上的两点,
上的两点,![]() ,
,![]() ,分别交
,分别交![]() 于
于![]() 两点,连
两点,连![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④ ![]() ,其中正确的是( )
,其中正确的是( )

A. ①②B. ①④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当涂大青山有较为丰富的毛竹资源,某企业已收购毛竹110吨,根据市场信息,将毛竹直接销售,每吨可获利100元;如果对毛竹进行粗加工,每天可加工8吨,每吨可获利1000元;如果进行精加工,每天可加工![]() 吨,每吨可获利5000元,由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售、为此研究了两种方案:
吨,每吨可获利5000元,由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售、为此研究了两种方案:
(1)方案一:将收购毛竹全部粗加工后销售,则可获利________元;
方案二:30天时间都进行精加工,未来得及加工的毛竹,在市场上直接销售,则可获利________元.
(2)是否存在第三种方案,将部分毛竹精加工,其余毛竹粗加工,并且恰好在30天内完成?若存在,求销售后所获利润;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是( )

A. 六年级40名男生身高的中位数在第153~158cm组
B. 可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cm
C. 九年级40名男生身高的中位数在第168~173cm组
D. 可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() 厘米.
厘米.
(1)如图一,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以4厘米/分的速度运动,同时点
点以4厘米/分的速度运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以6厘米/分的速度运动.求:①几分钟后
点以6厘米/分的速度运动.求:①几分钟后![]() 两点相遇? ②几分钟后
两点相遇? ②几分钟后![]() 两点相距20厘米?
两点相距20厘米?
(2)如图二,![]() 厘米,
厘米,![]() ,现将点
,现将点![]() 绕着点
绕着点![]() 以20度/分的速度顺时针旋转一周后停止,同时点
以20度/分的速度顺时针旋转一周后停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若
点运动,假若![]() 两点也能相遇,求点
两点也能相遇,求点![]() 的速度.
的速度.
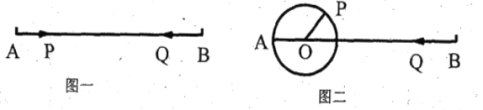
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4,点A,B,C在数轴上表示的数分别是1,![]() ,
,![]() ,点E到点B,C的距离相等,点P从点A出发,向左运动,速度是每秒0.3个单位长度.设运动的时间是t秒.
,点E到点B,C的距离相等,点P从点A出发,向左运动,速度是每秒0.3个单位长度.设运动的时间是t秒.
(1)点E表示的数是________;
(2)在t=3,t=4这两个时刻,使点P更接近原点O的时间是哪一个?
(3)若点P分别t=8,t=p两个不同的时刻,到点E的距离相等,求p的值;
(4)设点M在数轴上表示的数是m,点N在数轴上表示的数是n,式子________的值可以体现点M和点N之间的距离,这个式子的值越小,两个点的距离越近.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com