
分析 (1)首先根据a<0,b>0,且|a|>|b|,可得a<0<b,然后判断出-b<0<-a,即可推得a<-b<b<-a,据此求解即可;
(2)首先根据a<0,b>0,且a+b>0,可得a<0<b,|a|<|b|,然后判断出-b<0<-a,即可推得-b<a<-a<b,据此求解即可;
(3)根据已知得出a为负数,b为正数,|a|>|b|,求出a<-b<0,0<b<-a,即可得出答案.
解答 解:(1)∵a<0,b>0,且|a|>|b|,
∴a<0<b,
∴-b<0<-a,
∴a<-b<b<-a,
∴用“<”号把a、-a、b、-b连接起来为a<-b<b<-a;
(2)∵a<0,b>0,且a+b>0,
∴a<0<b,|a|<|b|,
∴-b<0<-a,
∴-b<a<-a<b,
∴用“<”号把a、-a、b、-b连接起来为-b<a<-a<b;
(3)∵ab<0,a+b<0,且a<0,
∴a为负数,b为正数,|a|>|b|,
∴a<-b<0,0<b<-a,
∴用“<”号把a、-a、b、-b连接起来为 a<-b<b<-a.
故答案为:a<-b<b<-a;-b<a<-a<b;a<-b<b<-a.
点评 此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
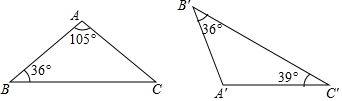 具备下列各组条件的两个三角形中,不一定相似的是( )
具备下列各组条件的两个三角形中,不一定相似的是( )| A. | 有一个角是36°的两个等腰三角形 | |
| B. | 有一个角为108°的两个等腰三角形 | |
| C. | 有一锐角对应相等的两个直角三角形 | |
| D. | 图中的△ABC与△A'B'C'相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com