|
|
|
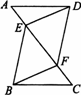
如图已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
|
|
|
答案:
解析:
|
证明:∵BE∥DF,
∴∠BEC=∠DFA,
在△ADF和△CBE中,
∵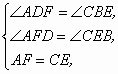
∴△ADF≌△CBE(AAS),
∴DF=BE
又∵BE∥DF,
∴四边形DEBF是平行四边形.
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列各组线段中,能组成直角三角形的是
|
| [ ] |
A. |
7,8,9
|
B. |
1,4,9
|
C. |
5,12,13
|
D. |
5,11,12
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
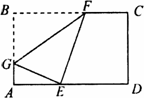
如图,折叠矩形纸片ABCD,使B点落在AD上点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
平行四边形ABCD的周长为32,且5AB=3BC,则对角线AC的取值范围为
|
| [ ] |
A. |
6<AC<10
|
B. |
6<AC<16
|
C. |
10<AC<16
|
D. |
4<AC<16
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在平行四边形ABCD中,O是对角线AC的中点,过O点作直线EF分别交BC、AD于点E、F.
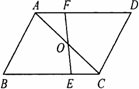
(1)求证:BE=DF;
(2)若AC、EF将平行四边形ABCD分成的四部分面积相等,指出E点的位置,并说明理由.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列说法正确的是
①平行四边形的两组对边分别相等;
②平行四边形的对角线相等;
③夹在平行线间的平行线段相等.
|
| [ ] |
A. |
①②
|
B. |
①②③
|
C. |
①③
|
D. |
②
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
在□ABCD中,∠A+∠C=200°,则∠B的度数是
|
| [ ] |
A. |
100°
|
B. |
160°
|
C. |
80°
|
D. |
60°
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.证明:四边形AEDF是菱形.
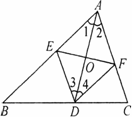
对于这道题,小林是这样证明的.
证明:因为AD平分∠BAC,所以∠1=∠2.
因为DE∥AC,所以∠2=∠3.
因为DF∥AB,所以∠1=∠4.
又AD=AD,所以△AED≌△AFD.
所以AE=AF,DE=DF.
所以四边形AEDF是菱形.
老师说小林的解题过程有错误,你能看出来吗?
(1)请你帮小林指出他的错误是什么.
(2)请你帮小林做出正确的解答.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为________.
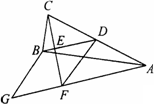
|
|
|
查看答案和解析>>

 备战中考寒假系列答案
备战中考寒假系列答案