
���� ��1��������ȫƽ����ʽ�ó�7+4$\sqrt{3}$=��2+$\sqrt{3}$��2����������ɣ�
��2��������ȫƽ����ʽ�ó�8-$\sqrt{60}$=��$\sqrt{5}$-$\sqrt{3}$��2����������ɣ�
��� �⣺��1��$\sqrt{7+4\sqrt{3}}$=$\sqrt{{��2+\sqrt{3}��}^{2}}$=2+$\sqrt{3}$��
��2��$\sqrt{8-\sqrt{60}}$=$\sqrt{8-2\sqrt{15}}$=$\sqrt{��\sqrt{5}-\sqrt{3}��^{2}}$=$\sqrt{5}$-$\sqrt{3}$��
���� ������Ҫ�����˶��θ�ʽ�Ļ��������ʣ�����Ӧ����ȫƽ����ʽ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
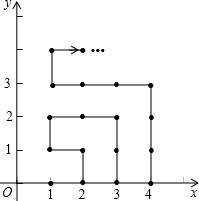 ��ƽ��ֱ������ϵ�У������ɸ�������ֱ�Ϊ�����ĵ㣬��˳��ͼ�С��������У��磨1��0������2��0������2��1������1��1����1��2������2��2������ô��23�����Ƕ��٣�
��ƽ��ֱ������ϵ�У������ɸ�������ֱ�Ϊ�����ĵ㣬��˳��ͼ�С��������У��磨1��0������2��0������2��1������1��1����1��2������2��2������ô��23�����Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��D��BC���е㣮AEƽ�֡�BAD��BC�ڵ�E����O��AB��һ�㣬��O��A��E���㣬��AB�ڵ�F����֪BC=16$\sqrt{2}$��AD=4��
��ͼ���ڡ�ABC�У�AB=AC��D��BC���е㣮AEƽ�֡�BAD��BC�ڵ�E����O��AB��һ�㣬��O��A��E���㣬��AB�ڵ�F����֪BC=16$\sqrt{2}$��AD=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com