
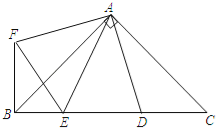
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF;②AE:BE=AD:CD;③△ABC的面积等于四边形AFBD的面积;④BE2+DC2=DE2⑤BE+DC=DE其中正确的是( )
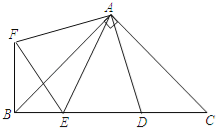
A. ①②④ B. ③④⑤ C. ①③⑤ D. ①③④
【答案】D
【解析】试题分析:①根据旋转的性质知∠CAD=∠BAF,AD=AF,∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°.∴∠EAF=45°,∴△AED≌△AEF;故本选项正确;
②∵AB=AC,∴∠ABE=∠ACD;∴当∠BAE=∠CAD时,△ABE∽△ACD,∴![]() =
=![]() ;当∠BAE≠∠CAD时,△ABE与△ACD不相似,即
;当∠BAE≠∠CAD时,△ABE与△ACD不相似,即![]() ≠
≠![]() ;∴此比例式不一定成立;故本选项错误;
;∴此比例式不一定成立;故本选项错误;
③根据旋转的性质知△ADC≌△AFB,∴S△ABC=S△ABD+S△ABF=S四边形AFBD,即三角形ABC的面积等于四边形AFBD的面积;故本选项正确;
④∵∠FBE=45°+45°=90°,∴BE2+BF2=EF2,∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD,又∵EF=DE,∴BE2+DC2=DE2,故本选项正确;
⑤根据①知道△AEF≌△AED,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,即BE+DC>DE,故本选项错误;
综上所述,正确的说法是①③④;
故选D.


科目:初中数学 来源: 题型:
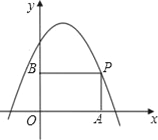
【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械厂一月份生产零件50万个,三月份生产零件72万个,则该机械厂二、三月份生产零件数量的月平均增长率为( )
A.2%B.5%C.10%D.20%
查看答案和解析>>
科目:初中数学 来源: 题型:
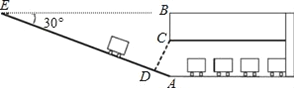
【题目】某商场为方便顾客停车,决定设计一个地下停车场,为了测得该校地下停车场的限高CD,在施工时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,BC=8
(1)求对角线AC的长;
(2)点E是线段CD上的一点,把△ADE沿着直线AE折叠.点D恰好落在线段AC上,点F重合,求线段DE的长. 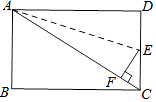
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一点C,过点C分别作CA⊥x轴,CB⊥y轴,点A、B是垂足.
定义:若长方形OACB的周长与面积的数值相等,则点C是平面直角坐标系中的平衡点.
(1)请判断下列是平面直角坐标系中的平衡点的是;(填序号)
①E(1,2)②F(﹣4,4)
(2)若在第一象限中有一个平衡点N(4,m)恰好在一次函数y=﹣x+b(b为常数)的图象上;
①求m、b的值;
②一次函数y=﹣x+b(b为常数)与y轴交于点D,问:在这函数图象上,是否存在点M,使S△OMD=3S△OND , 若存在,请直接写出点M的坐标;若不存在,请说明理由.
(3)过点P(0,﹣2),且平行于x轴的直线上有平衡点Q吗?若有,请求出平衡点Q的坐标;若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.

(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com