
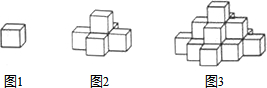
分析 分前后左右四个部分查出涂色的面,从上面分横向与纵向两个方向查出需涂色的面,然后相加,利用求和公式计算即可得解.
解答 解:由图形可知:从正面看,需涂色的面有:1+3+5+…+(2n-1)=n2,
所以,从前、后、左、右看,需涂色的面有4n2,
从上面看,需涂色的面有:1+3+5+…+(2n-1)+…5+3+1=2n2-2n+1,
所以,第n个叠放的图形中,涂上颜色的面有:6n2-2n+1;
因此第7个叠放的图形中,涂到油漆部分的面积是6×72-2×7+1=281.
故答案为:281.
点评 本题考查图形的变化规律,注意确定正方体的个数与涂色面数时按照一定的顺序查找方可做到不重不漏,也是解题的关键.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
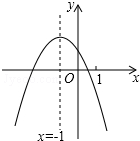 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc<0;②4ac-b2<0;③4a-2b+c=0;④am2+bm<a-b(m≠-1),其中正确结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc<0;②4ac-b2<0;③4a-2b+c=0;④am2+bm<a-b(m≠-1),其中正确结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
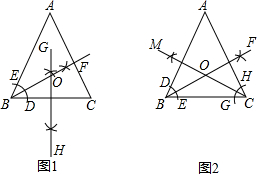 △ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.
△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.| A. | 两人都对 | B. | 两人都不对 | C. | 甲对,乙不对 | D. | 乙对,甲不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 64,100 | B. | 64,76 | C. | 76,64 | D. | 64,84 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
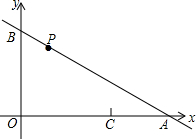 如图所示,在直角坐标系中,直线l与x轴、y轴相交于A、B两点,已知点A的坐标是(8,0),点B的坐标是(0,6).
如图所示,在直角坐标系中,直线l与x轴、y轴相交于A、B两点,已知点A的坐标是(8,0),点B的坐标是(0,6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com