
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( ) 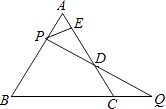
A.![]()
B.![]()
C.![]()
D.不能确定
【答案】B
【解析】解:过P作PM∥BC,交AC于M;
∵△ABC是等边三角形,且PM∥BC,
∴△APM是等边三角形;
又∵PE⊥AM,
∴AE=EM= ![]() AM;(等边三角形三线合一)
AM;(等边三角形三线合一)
∵PM∥CQ,
∴∠PMD=∠QCD,∠MPD=∠Q;
又∵PA=PM=CQ,
在△PMD和△QCD中
∴△PMD≌△QCD(AAS);
∴CD=DM= ![]() CM;
CM;
∴DE=DM+ME= ![]() (AM+MC)=
(AM+MC)= ![]() AC=
AC= ![]() ,故选B.
,故选B.
【考点精析】通过灵活运用平行线的性质和等边三角形的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等边三角形的三个角都相等并且每个角都是60°即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
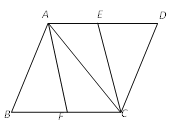
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1)求证△ABF ≌ △CDE;
(2)若AB=AC,求证四边形AFCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠F= . 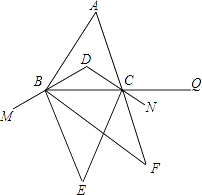
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在![]() 中,试说明
中,试说明![]() .
.
分析:通过画平行线,将![]() 、
、![]() 、
、![]() 作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
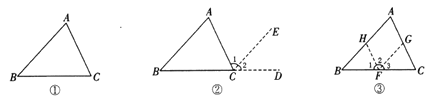
解:如图②,延长![]() 到点
到点![]() ,过点
,过点![]() 作
作![]() //
//![]() .
.
因为![]() //
//![]() (作图所知),
(作图所知),
所以![]() ,
,![]() (两直线平行,同位角、内错角相等).
(两直线平行,同位角、内错角相等).
又因为![]() (平角的定义),
(平角的定义),
所以![]() (等量代换).
(等量代换).
如图③,过![]() 上任一点
上任一点![]() ,作
,作![]() //
//![]() ,
, ![]() //
//![]() ,这种添加辅助线的方法能说
,这种添加辅助线的方法能说![]() 吗?并说明理由.
吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com