
分析 (1)利用y=-10x+500,将x30代入求出答案;
(2)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价-进价)×销售量,从而列出关系式,求出最值.
解答 解:(1)由题意可得:y=-10×30+500=200(本),
答:当销售单价为30元时,小王销售畅销书每月的营业额为200本;
(2)设月利润为w,
由题意得:w=(x-20)×y,
=(x-20)•(-10x+500)
=-10x2+700x-10000
=-10(x-35)2+2250,
故当x=35时,w最大=2250(元).
答:小王销售这种畅销书每月可获得的最大利润为2250元.
点评 此题考查了二次函数的应用,将实际问题转化为求函数最值问题是解题关键.


科目:初中数学 来源: 题型:选择题
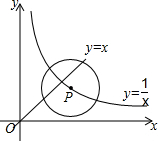 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )| A. | 1≤x≤$\sqrt{2}$ | B. | $\sqrt{2}-1≤x≤\sqrt{2}$ | C. | $\sqrt{2}-1≤x≤1$ | D. | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$.
如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -3 | -2 | -1 | 0 |
| y | 0 | -3 | -4 | -3 |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
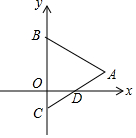 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D为AC边的中点,则点D的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D为AC边的中点,则点D的坐标为( )| A. | (1,0) | B. | (2$\sqrt{3}$,0) | C. | (2,0) | D. | ($\sqrt{3}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
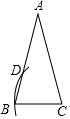 如图,在等腰△ABC中,AB=AC,BC=6,∠BAC=30°,以点C为圆心,CB长为半径画弧交AB于点D,则弧BD的长为( )
如图,在等腰△ABC中,AB=AC,BC=6,∠BAC=30°,以点C为圆心,CB长为半径画弧交AB于点D,则弧BD的长为( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | $\frac{25π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com