
分析 根据条件中的运算规律,就可得到f(n)=1+$\frac{2}{n}$=$\frac{n+2}{n}$,然后利用这个规律就可求出f(1)•f(3)•f(5)•f(7)…f(99)的值.
解答 解:利用以上得出的运算规律,可得f(n)=1+$\frac{2}{n}$=$\frac{n+2}{n}$;
f(1)•f(3)•f(5)•f(7)…f(99)=$\frac{3}{1}$×$\frac{5}{3}$×$\frac{7}{5}$×$\frac{9}{7}$×…×$\frac{101}{99}$=101.
故答案为$\frac{n+2}{n}$,101.
点评 本题属于规律探究题,运用归纳得出的结论可以化简求值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )
如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )| A. | 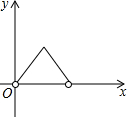 | B. |  | C. | 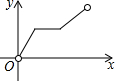 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 江夏体育馆是市民娱乐,休闲的中心.现在体育馆要建一处公共服务设施,使它到三个市民活动区域A、B、C的距离相等.若三个市民活动区域A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置(保留作图痕迹,不要求写作法)
江夏体育馆是市民娱乐,休闲的中心.现在体育馆要建一处公共服务设施,使它到三个市民活动区域A、B、C的距离相等.若三个市民活动区域A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置(保留作图痕迹,不要求写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com