
 如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P的速度都是1cm/s,点Q的速度都是2cm/s当点P到达点B时,P、Q两点停止.当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形. 分析 先分别表示出BP,BQ的值,当∠BQP和∠BPQ分别为直角时,由等边三角形的性质就可以求出结论.
解答 解:∵△ABC是等边三角形,
∴AB=BC=3cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=3-t,BQ=2t,
∴3-t=2×2t,
解得t=$\frac{3}{5}$;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴2t=2(3-t),
解得t=$\frac{3}{2}$.
答:当t=$\frac{3}{5}$或$\frac{3}{2}$时,△PBQ是直角三角形.
故答案为:$\frac{3}{5}$或$\frac{3}{2}$.
点评 本题考查了等边三角形的性质的运用,30°角的直角三角形的性质的运用,利用分类讨论是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017届辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
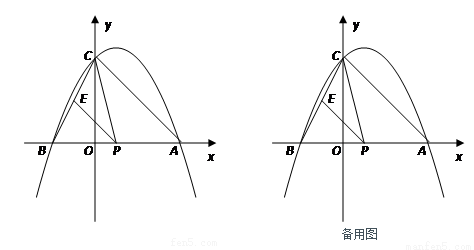
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com