练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，△ABC为⊙O的内接等腰三角形，底边AB为，⊙O的半径为4，则∠C度数为___.

    【答案】600或1200

    【解析】过圆心作AB的垂线，在构建的直角三角形中，易求得圆心角∠AOB的度数，由此可求出∠C的度数.（注意∠C所对的弧可能是优弧，也可能是劣弧）

    解：如图，连接OA、OB，过O作OD⊥于AB于D.

    在Rt△OAD中，D=，OA=2，

    ∴sin∠AOD==，

    ∴∠AOD=60°，∠AOB=120°.

    点C的位置有两种情况：

    ①当点C在如图位置时，∠C=∠AOB=60°；

    ②当点C在E点位置时，∠C=∠E=180°-∠F=120°.

    故答案为：600或1200.

    “点睛”本题主要考查了垂径定理以及解直角三角形的应用，注意点C的位置有两种情况，不要漏解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】以下问题，不适合用全面调查的是（ ）

    A.旅客上飞机前的安检

    B.学校招聘教师，对应聘人员的面试

    C.了解全校学生的课外读书时间

    D.了解一批灯泡的使用寿命

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两件服装进价共500元商店决定把甲服装按进价提高50%标价，乙服装按进价提高40%标价，如果两件服装均按标价的九折出售，这样商店获利共157元。甲、乙两件服装进价分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，(1)∵∠A=_____(已知)，

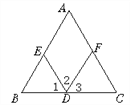
    ∴AC∥ED( )

    (2)∵∠2=_____(已知)，

    ∴AC∥ED( )

    (3)∵∠A+_____=180°(已知)，

    ∴AB∥FD( )

    (4)∵AB∥_____(已知)，

    ∴∠2+∠AED=180°( )

    (5)∵AC∥_____(已知)，

    ∴∠C=∠1( )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了增强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过10吨时，水价为每吨1．2元，超过10吨时，超过的部分按每吨1．8元收费，该市某户居民5月份用水x吨（x＞10），应交水费y元，则y关于x的函数关系式是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算（直接写出结果）:①a·a3=__________． ②(b3)4=________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据中若最小数与平均数相等，那么这组数据的方差为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC，BC于点D，E，且

    （1）求证：AB=AC.

    （2）若∠C=70°，求的度数.

    （3）如图2，点F在⊙O上， ，连结DF，DE.求证：∠ADF=∠CDE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】⊙O的直径为4，点A到圆心O距离为3．则（　　）

    A.点A在⊙O外B.点A在⊙O上

    C.点A在⊙O内D.点A与⊙O的位置关系不能确定

    查看答案和解析>>

    同步练习册答案