
 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
, 的解析式;
的解析式; ,使点
,使点 到
到 、
、 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由; 轴的一条直线交抛物线于
轴的一条直线交抛物线于 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与 轴相切,求此圆的半径.
轴相切,求此圆的半径.
 代入
代入 ,
, .
. ,
, 代入
代入 ,
, .……….(1)
.……….(1) 是对称轴,
是对称轴, . (2)
. (2)  ,
,  .
. .
. 与对称轴的交点
与对称轴的交点 即为到
即为到 的距离之差最大的点.
的距离之差最大的点. 点的坐标为
点的坐标为 ,
, 点的坐标为
点的坐标为 ,
, 的解析式是
的解析式是 ,
, ,
, 的坐标
的坐标 .
.  、
、 ,所求圆的半径为r,
,所求圆的半径为r, ,……………(1)
,……………(1) ,
, . ……………(2)
. ……………(2) .………(3)
.………(3)  代入解析式
代入解析式 ,
, ,…………(4)
,…………(4) .
. 时,
时, ,
, ,
,  (舍去),
(舍去), 时,
时, ,
, ,
,  (舍去).
(舍去). 或
或 .
. =1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.
=1,然后可将B点坐标代入抛物线的解析式中,联立由对称轴得出的关系式即可求出抛物线的解析式.

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, .它的顶点
.它的顶点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点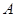 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点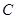 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
 的度数.
的度数. 在
在 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度. 与时间
与时间 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标. 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿 边运动时,
边运动时,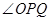 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时,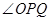 的大小随着时间
的大小随着时间 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使 的点
的点 有几个?请说明理由.
有几个?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
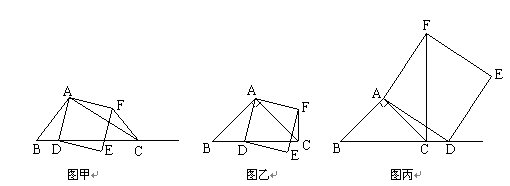
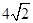 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com