
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 平分
平分![]() ,过
,过![]() 点作
点作![]() 于
于![]() 点.
点.
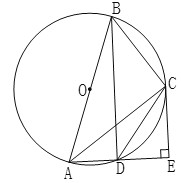
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)如图1(见解析),连接OC、OD,先由圆周角定理得![]() ,从而可得
,从而可得![]() ,再根据圆周角定理和圆心角定理可得
,再根据圆周角定理和圆心角定理可得![]() ,由此可得
,由此可得![]() 垂直平分
垂直平分![]() ,即有
,即有![]() ,从而可证
,从而可证![]() ,最后根据圆的切线的判定定理可证;
,最后根据圆的切线的判定定理可证;
(2)方法一:如图2(见解析),延长![]() 交
交![]() 的延长线于
的延长线于![]() 点,先利用三角形全等求出AF和CF的长,再通过证出两个三角形相似即可得;方法二:如图1(见解析),先利用
点,先利用三角形全等求出AF和CF的长,再通过证出两个三角形相似即可得;方法二:如图1(见解析),先利用![]() 求出CE和AE的长,再利用勾股定理求出DE的长,最后根据线段的和差即可得.
求出CE和AE的长,再利用勾股定理求出DE的长,最后根据线段的和差即可得.
(1)如图1,连接![]()
![]() 是
是![]() 的直径
的直径
![]()
![]() 于
于![]() 点
点
![]()
![]()
![]()
![]() 平分
平分![]() ,即
,即![]()
![]() (圆周角定理)
(圆周角定理)
![]() (圆心角定理)
(圆心角定理)
![]() 垂直平分
垂直平分![]() ,即有
,即有![]()
![]()
∴CE是![]() 的切线;
的切线;
(2)∵AB是![]() 的直径
的直径
![]()
![]()
由题(1)已证![]()
方法一: 如图2,延长![]() 交
交![]() 的延长线于
的延长线于![]() 点
点
![]()
![]()
![]()
![]() ,
,![]() (圆内接四边形的对角互补)
(圆内接四边形的对角互补)
![]()
又![]()
![]()
![]()
![]()
![]()
![]() ;
;
方法二:如图1,![]()
![]()
![]()
![]()
![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
![]() .
.
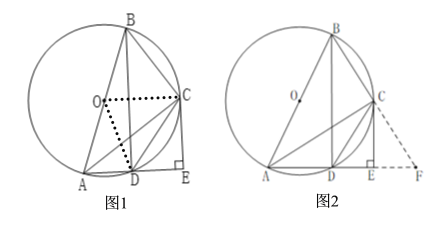


科目:初中数学 来源: 题型:
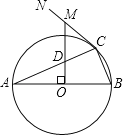
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
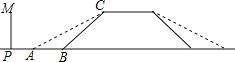
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面![]() 的坡度为
的坡度为![]() ,文化墙
,文化墙![]() 在天桥底部正前方8米处(
在天桥底部正前方8米处(![]() 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为
的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为![]() .(参考数据:
.(参考数据:![]() ,
,![]() )
)
(1)若新坡面坡角为![]() ,求坡角
,求坡角![]() 度数;
度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙![]() 是否需要拆除?请说明理由.
是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
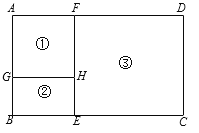
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
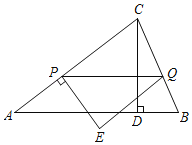
【题目】如图,在△ABC中,AB=AC=5,CD⊥AB于点D,CD=3.点P从点A出发沿线段AC以每秒1个单位的速度向终点C运动.过点P作PQ∥AB交BC于点Q,过点P作AC的垂线,过点Q作AC的平行线,两线交于点E.设点P的运动时间为t秒.
(1)求线段PQ的长.(用含t的代数式表示)
(2)当点E落在边AB上时,求t的值.
(3)当△PQE与△ACD重叠部分图形是四边形时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
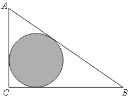
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com