
 如图,是10×8的网格,网格中每个小正方形的边长均为1,线段AB的端点都在小正方形的顶点上,
如图,是10×8的网格,网格中每个小正方形的边长均为1,线段AB的端点都在小正方形的顶点上,分析 (1)利用勾股定理计算出AB=5,象AB一样不在一条格线上可作出AC=5,则△ABC为等腰直角三角形;与A在同一格线上易作AD=5,则△ABD为等腰钝角三角形;
(2)根据三角形面积公式和四边形ABCD的面积=S△ABC+S△ADC进行计算.
解答 解:(1)如图,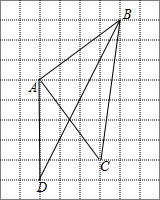
(2)如图,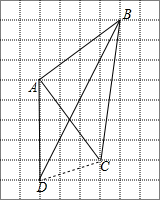
四边形ABCD的面积=S△ABC+S△ADC=$\frac{1}{2}$×5×5+$\frac{1}{2}$×5×3=20.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此题的关键是充分利用网格的特点和用勾股定理计算出AB的长.


科目:初中数学 来源: 题型:填空题
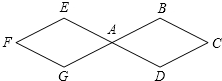 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
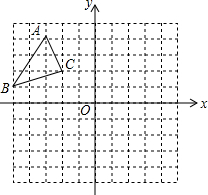 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
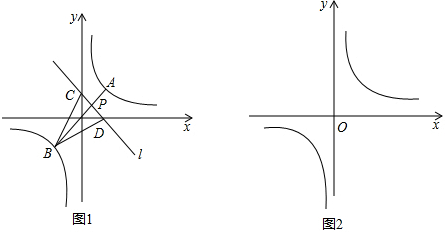
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
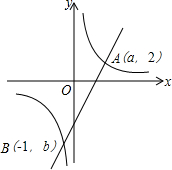 如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
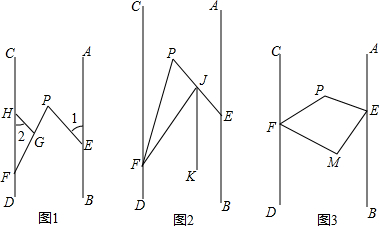
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )
如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )| A. | 6 | B. | 12 | C. | $\frac{12\sqrt{5}}{5}$ | D. | 6$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com