
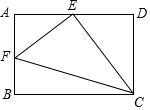
 如图,在矩形ABCD中,E是AD的中点,EF⊥EC交AB于点F,连接FC,问:△AEF与△ECF相似吗?若相似,探求你的结论,若不相似,请说明理由.
如图,在矩形ABCD中,E是AD的中点,EF⊥EC交AB于点F,连接FC,问:△AEF与△ECF相似吗?若相似,探求你的结论,若不相似,请说明理由. 分析 先证明Rt△AEF∽Rt△DCE得到$\frac{EF}{CE}$=$\frac{AF}{DE}$,再利用AE=DE得到$\frac{EF}{CE}$=$\frac{AF}{AE}$,则利用比例性质得$\frac{EF}{AF}$=$\frac{CE}{EA}$,然后利用两组对应边的比相等且夹角对应相等的两个三角形相似可判断△AEF∽△ECF.
解答 解:△AEF与△ECF相似.理由如下:
∵EF⊥EC,
∴∠CEF=90°,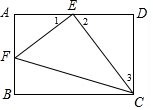
∴∠1+∠2=90°,
∵∠1+∠2=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∴Rt△AEF∽Rt△DCE,
∴$\frac{EF}{CE}$=$\frac{AF}{DE}$,
∵E是AD的中点,
∴AE=DE,
∴$\frac{EF}{CE}$=$\frac{AF}{AE}$,
∴$\frac{EF}{AF}$=$\frac{CE}{EA}$,
而∠A=∠CEF,
∴△AEF∽△ECF.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了相似三角形的性质和矩形的性质.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x | B. | y=x2 | C. | y=2x-1 | D. | y=x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
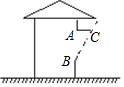 如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为( )
如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为( )| A. | 1.8tan80°m | B. | 1.8cos80°m | C. | $\frac{1.8}{sin80°}$ m | D. | $\frac{1.8}{tan80°}$ m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )
如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )| A. | 5 | B. | 7 | C. | 12 | D. | $\sqrt{26}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com