
分析 本题应对代数式进行去括号,合并同类项,将代数式化为最简式,然后把x、y的值代入即可.注意去括号时,如果括号前是负号,那么括号中的每一项都要变号;合并同类项时,只把系数相加减,字母与字母的指数不变.
解答 解:∵A=4x2-4xy+y2,B=x2+xy-5y2,
∴(3A-2B)-(2A+B)
=(12x2-12xy+3y2-2x2-2xy+10y2)-(8x2-8xy+2y2+x2+xy-5y2)
=12x2-12xy+3y2-2x2-2xy+10y2-8x2+8xy-2y2-x2-xy+5y2
=x2-7xy+16x2,
当x=-5,y=-2时,
原式=(-5)2-7×(-5)×(-2)+16×(-2)2=19.
点评 本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.


科目:初中数学 来源: 题型:解答题
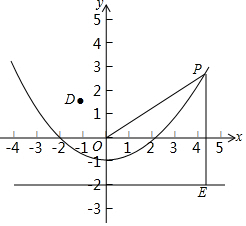 抛物线的解析式为y=$\frac{1}{4}$x2-1,D点坐标为(-1,$\frac{3}{2}$),经过点C(0,-2)的直线l与x轴平行,P(m,n)是抛物线y=$\frac{1}{4}$x2-1上的动点.
抛物线的解析式为y=$\frac{1}{4}$x2-1,D点坐标为(-1,$\frac{3}{2}$),经过点C(0,-2)的直线l与x轴平行,P(m,n)是抛物线y=$\frac{1}{4}$x2-1上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
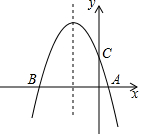 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,与y轴相交于点C,请完成下面的填空:
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点,与y轴相交于点C,请完成下面的填空:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
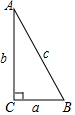 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1、3、-1 | B. | -1、3、1 | C. | -1、-3、-1 | D. | 1、-3、-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com