
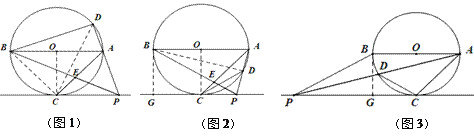
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

【答案】(1)45°;(2)见解析;(3)①∠ACD=15°;∠ACD=105°;∠ACD=60°;∠ACD=120°
②36或![]() .
.
【解析】试题分析:(1)易得△ABC是等腰直角三角形,从而∠BAC=∠CBA=45°;
(2)分当 B在PA的中垂线上,且P在右时;B在PA的中垂线上,且P在左;A在PB的中垂线上,且P在右时;A在PB的中垂线上,且P在左时四中情况求解;
(3)①先说明四边形OHEF是正方形,再利用△DOH∽△DFE求出EF的长,然后利用割补法求面积;②根据△EPC∽△EBA可求PC=4,根据△PDC∽△PCA可求PD PA=PC2=16,再根据S△ABP=S△ABC得到![]() ,利用勾股定理求出k2,然后利用三角形面积公式求解.
,利用勾股定理求出k2,然后利用三角形面积公式求解.
(1)解:(1)连接BC,
∵AB是直径,
∴∠ACB=90°.
∴△ABC是等腰直角三角形,
∴∠BAC=∠CBA=45°;
(2)解:∵![]() ,∴∠CDB=∠CDP=45°,CB= CA,
,∴∠CDB=∠CDP=45°,CB= CA,
∴CD平分∠BDP
又∵CD⊥BP,∴BE=EP,
即CD是PB的中垂线,
∴CP=CB= CA,
(3)① (Ⅰ)如图2,当 B在PA的中垂线上,且P在右时,∠ACD=15°;
(Ⅱ)如图3,当B在PA的中垂线上,且P在左,∠ACD=105°;
(Ⅲ)如图4,A在PB的中垂线上,且P在右时∠ACD=60°;
(Ⅳ)如图5,A在PB的中垂线上,且P在左时∠ACD=120°
②(Ⅰ)如图6,![]() ,
,![]()
![]()
![]()
![]() .
.
(Ⅱ)如图7,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设BD=9k,PD=2k,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )

A. AB=DB,∠ A=∠ D B. DB=AB,AC=DE C. AC=DE,∠C=∠E D. ∠ C=∠ E,∠ A=∠ D
查看答案和解析>>
科目:初中数学 来源: 题型:
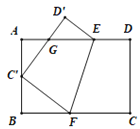
【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G.若G是CD的中点,则BC的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春夏来临之际,天气开始暖和,某商家抓住商机,在三月份力推甲、乙两款儿童衬衣.已知三月份甲款衬衣的销售总额为6000元,乙款衬衣的销售总额为8100元,乙款衬衣的单价是甲款衬衣单价的1.5倍,乙款衬衣的销售数量比甲款衬衣的销售数量少5件.
(1)求三月份甲款衬衣的单价是多少元?
(2)四月份,该商家准备销售甲、乙两款衬衣共200件,为了加大推销力度,将甲款衬衣的单价在三月份的基础上下调了20%,乙款衬衣的单价在三月份的基础上打五折销售.要使四月份的总销售额不低于18720元,则该商家至少要卖出甲款衬衣多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com