
【题目】(2016广东省梅州市第20题)
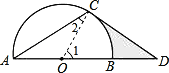
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、连接OC,根据等腰三角形的性质得出∠CAD=∠D=30°,根据OA=OC得出∠2=∠CAD =30°,从而得出∠OCD=∠ACD —∠ACO=90°;(2)、首先求出扇形BOC的面积,根据Rt△OCD的三角函数得出CD的长度,从而求出Rt△OCD的面积,然后求出阴影部分的面积.
试题解析:(1)、连接OC. ∵AC=CD,∠ACD=120°, ∴∠CAD=∠D=30°.
∵OA=OC, ∴∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° )
∴∠OCD=∠ACD —∠ACO=90°,即OC⊥CD. ∴CD是⊙O的切线.
(2)、由(1)知∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° ), ∴∠1=60°.(或∠COD =60°)
∴![]() . 在Rt△OCD中,∵
. 在Rt△OCD中,∵![]() ,
,![]() ∴
∴![]() .
.
∴![]() ∴图中阴影部分的面积为
∴图中阴影部分的面积为![]()


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
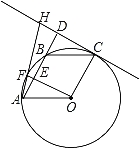
【题目】(2016湖北省荆州市第23题)如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=6﹣3![]() ,求EF和半径OA的长.
,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用全面调查的是( )
A. 了解明德集团所有中学生的视力情况
B. 了解某校七(4)班学生校服的尺码情况
C. 调查北京2017年的游客流量
D. 调查中国“2018俄罗斯世界杯”栏目的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在二次函数y=x2+bx+c中,函数y与自变量x之间的部分对应值如下表所示:若点A(﹣1,m),B(6,n),则m_____n.(选填“>”、“<”或“=”)
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | 3 | 0 | ﹣1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A1B1C1是位似图形,它们在位似中心的同侧,其面积比为4∶9,已知位似中心O与A的距离为2,则A到A1的距离为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足![]() +(c-8)2=0.
+(c-8)2=0.
![]()
(1) a = ,b = ,c = .
(2) 若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4) 请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com