
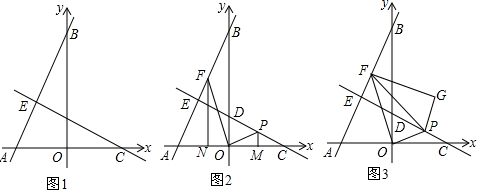
分析 (1)根据自变量与函数值的对应关系,可得A点坐标,根据OA=OC,可得C点坐标,根据互相垂直的两直线间的关系,可得直线CD解析式中一次项的系数,根据待定系数法,可得CD的解析式;
(2)根据互相垂直的两直线的一次项系数的乘积为-1,可得p与f的关系,根据两点间的距离,可得答案;
(3)根据待定系数法,可得PF的解析式,根据互相垂直的两直线的一次项系数的乘积为-1,可得直线OG的解析式,根据OG的中点在直线OG上、在直线PF上,可得G点坐标,根据直线AB与CD的交点,可得E点坐标,根据平行于x轴的直线上两点间的距离等于大的横坐标减小的横坐标,可的关于p的方程,根据解方程,可得答案.
解答 解:(1)过直线y=2x+10
当x=0时,y=2×0+10,B点坐标为(0,10),
当y=0时,x=-$\frac{10}{2}$=-5,A点坐标为(-5,0).
OC=OA,则C点坐标为(5,0).
由CD⊥AB,得kCD=-$\frac{1}{2}$,
设直线CD的解析式为y=-$\frac{1}{2}$2x+b,
将C点代入解析式,得
0=-$\frac{1}{2}$×5+b,解得 b=$\frac{5}{2}$.
CD的解析式为y=-$\frac{1}{2}$x+$\frac{5}{2}$;
(2)设P点坐标为(p,-$\frac{1}{2}$p+$\frac{5}{2}$)
那么kPO=$\frac{-\frac{1}{2}p+\frac{5}{2}}{p}$
由OP⊥OF,得kOF=$\frac{-p}{-\frac{1}{2}p+\frac{5}{2}}$
设F点坐标为(f,2f+10)
可知kOF=$\frac{2f+10}{f}$
那么有$\frac{-p}{-\frac{1}{2}p+\frac{5}{2}}$=$\frac{2f+10}{f}$
整理得到p-f=5
由题意,并观察图形可得到MN的距离为p-f=5;
(3)由(2)可知f=p-5
那么F点坐标为((p-5),2(p-5)+10),即F((p-5),2p)
设直线PF解析式为y=kx+b,将F、P坐标代入解析式,得$\left\{\begin{array}{l}{2p=k(p-5)+b}\\{-\frac{1}{2}p+\frac{5}{2}=pk+b}\end{array}\right.$,解得
$\left\{\begin{array}{l}{k=\frac{1-p}{2}}\\{b=\frac{{p}^{2}-2p+5}{2}}\end{array}\right.$,
即PF的解析式为
y=$\frac{1-p}{2}$x+$\frac{{p}^{2}-2p+5}{2}$.
由G关于PF为O的对称点,得
kOG=$\frac{2}{P-1}$
设OG直线解析式为y=$\frac{2}{p-1}$x,
设G点坐标为(xG,yG),
又知道点OG的中点H($\frac{{x}_{G}}{2}$,$\frac{{y}_{G}}{2}$)在直线PF上,
代入OG、PF解析式,得$\left\{\begin{array}{l}{\frac{{y}_{G}}{2}=\frac{2}{p-1}•\frac{{x}_{G}}{2}}\\{\frac{{y}_{G}}{2}=\frac{1-p}{2}•\frac{{x}_{G}}{2}+\frac{{p}^{2}-2p+5}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{G}=2p-2}\\{{y}_{G}=4}\end{array}\right.$.
根据CD、AB解析式可求得E点坐标为(-3,4)
那么EG=xG+3=2p-2+3=7
解得p=3,-$\frac{1}{2}$p+$\frac{5}{2}$=-$\frac{1}{2}$×3+$\frac{5}{2}$=1,
P点坐标为(3,1).
点评 本题考查了一次函数综合题,(1)利用了互相垂直的两直线间的关系得出直线CD一次项的系数是解题关键;(2)利用互相垂直的两直线的一次项系数的乘积为-1得出关于p、f的方程式解题关键;(3)利用待定系数法求函数解析式,互相垂直的两直线的一次项系数的乘积为-1,解方程组求交点坐标,线段的中点在线段的对称轴上,平行于x轴的直线上两点间的距离.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
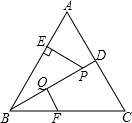 如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.
如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
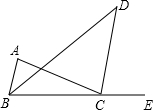 如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上.
如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
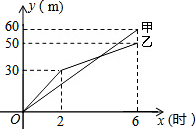 有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:
有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
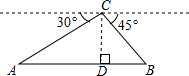 马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)
马航MH370失联以来,中国政府高度重视,每天军方派遣多架飞机、多艘军舰进行海上联合搜寻,某一天,从飞机C处测得A、B两艘军舰的俯角分别为30°、45°,此时飞机C处的高度CD为400米,点A,D,B在同一直线上,则A、B两艘军舰的距离是400($\sqrt{3}$+1)米.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com