
【题目】阅读理解
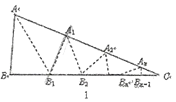
如图1,![]() 中,沿
中,沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下部分沿
折叠,剪掉重叠部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;……;将余下部分沿
折叠,剪掉重叠部分;……;将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,无论折叠多少次,只要最后一次恰好重合,我们就称
重合,无论折叠多少次,只要最后一次恰好重合,我们就称![]() 是
是![]() 的好角.
的好角.
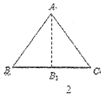
情形一:如图2,沿等腰三角形![]() 顶角
顶角![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合;
重合;
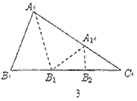
情形二:如图3,沿![]() 的
的![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下的部分沿
折叠,剪掉重叠部分;将余下的部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点
与点![]() 重合.
重合.
探究发现
(1)![]() 中,
中,![]() ,经过两次折叠,问
,经过两次折叠,问![]()
![]() 的好角(填写“是”或“不是”);
的好角(填写“是”或“不是”);
(2)若经过三次折叠发现![]() 是
是![]() 的好角,请探究
的好角,请探究![]() 与
与![]() (假设
(假设![]() )之间的等量关系 ;
)之间的等量关系 ;
根据以上内容猜想:若经过![]() 次折叠
次折叠![]() 是
是![]() 的好角,则
的好角,则![]() 与
与![]() (假设
(假设![]() )之间的等量关系为 ;
)之间的等量关系为 ;
应用提升:
(3)小丽找到一个三角形,三个角分别为![]() ,
,![]() ,
,![]() ,发现 是此三角形的好角;
,发现 是此三角形的好角;
(4)如果一个三角形的最小角是![]() ,且满足该三角形的三个角均是此三角形的好角;
,且满足该三角形的三个角均是此三角形的好角;
则此三角形另外两个角的度数 .
【答案】(1)是;(2)![]() ;
;![]() ;(3)
;(3)![]() 和
和![]() ;(4)另外两个角的度数分别为
;(4)另外两个角的度数分别为![]() 和
和![]()
【解析】
(1)由沿![]() 的平分线
的平分线![]() 折叠,得
折叠,得![]() ,且
,且![]() ,沿
,沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与
与![]() 重合,可得
重合,可得![]() ,即可证
,即可证![]() .
.
(2)由沿![]() 的平分线
的平分线![]() 折叠,得
折叠,得![]() ,由将余下部分沿
,由将余下部分沿![]() 的平分线
的平分线![]() 折叠,得
折叠,得![]() ,最后沿
,最后沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,得
重合,得![]() ,由
,由![]() ,可证
,可证![]() ;由小丽展示的情形一当
;由小丽展示的情形一当![]() 时;由探究(1)当
时;由探究(1)当![]() 时;由探究(2)当
时;由探究(2)当![]() 时,它们的
时,它们的![]() 均是
均是![]() 的好角;可推经过
的好角;可推经过![]() 次折叠,
次折叠,![]() 是
是![]() 的好角,则
的好角,则![]() 与
与![]() 的等量关系为
的等量关系为![]() .
.
(3)由(2)得![]() ,可计算
,可计算![]() 是
是![]() 的好角.
的好角.
(4)由(2)知![]() ,
,![]() 是
是![]() 的好角,已知中一个三角形的最小角是
的好角,已知中一个三角形的最小角是![]() ,且这个三角形三个角均是
,且这个三角形三个角均是![]() 的好角,可设另外两个角为
的好角,可设另外两个角为![]() 、
、![]() ,(其中
,(其中![]() 都是正整数),依题意列式
都是正整数),依题意列式![]() ,可求解得.
,可求解得.
(1)![]() 中,
中,![]() ,经过两次折叠,
,经过两次折叠,![]() 是
是![]() 的好角;
的好角;
理由如下:![]() 沿
沿![]() 的平分线
的平分线![]() 折叠,
折叠,
![]() ;
;
![]() 将余下部分沿
将余下部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与
与![]() 重合,
重合,
![]() ;
;
![]() ;
;
![]() ,
,
故答案是:是;
(2)在![]() 中,沿
中,沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分;将余下部分沿
折叠,剪掉重复部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,将余下部分沿
折叠,剪掉重复部分,将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,则
重合,则![]() 是
是![]() 的好角.
的好角.
证明:![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
由小丽展示的情形一知,当![]() 时,
时,![]() 是
是![]() 的好角;
的好角;
由探究(1)知,当![]() 时,
时,![]() 是
是![]() 的好角;
的好角;
由探究(2)知,当![]() 时,
时,![]() 是
是![]() 的好角;
的好角;
故若经过![]() 次折叠,
次折叠,![]() 是
是![]() 的好角,则
的好角,则![]() 与
与![]() 的等量关系为
的等量关系为![]() .
.
故答案为:![]() .
.
(3)由(2)知,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的好角.
的好角.
故答案为:![]() .
.
(4)由(2)知![]() ,
,![]() 是
是![]() 的好角,一个三角形的最小角是
的好角,一个三角形的最小角是![]() ,且这个三角形三个角均是
,且这个三角形三个角均是![]() 的好角,可设另外两个角为
的好角,可设另外两个角为![]() 、
、![]() ,(其中
,(其中![]() 都是正整数).
都是正整数).
依题意得![]() ,
,
化简得![]() ,
,
![]() 都是正整数,
都是正整数,
![]()
![]() 都是17的整数因子,
都是17的整数因子,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
即该三角形的另外两个角是:![]() 和
和![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
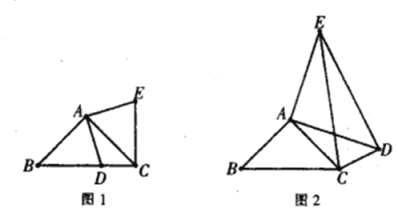
【题目】如图1 ,在![]() 中,
中,![]()
![]() 是
是![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
(发现问题)
(1)如图1 ,通过图形旋转的性质,可知![]() _______,
_______,![]() 度;
度;
(解决问题)
(2)如图1,证明![]() ;
;
(拓展延伸)
如图2,在![]() 中,
中,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
(3)若![]() 求的
求的![]() 长.
长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:
已知,在菱形ABCD中,BD为对角线,![]() ,AB=4,将菱形ABCD绕顶点A顺时针旋转,旋转角为
,AB=4,将菱形ABCD绕顶点A顺时针旋转,旋转角为![]() (单位°).旋转后的菱形为
(单位°).旋转后的菱形为![]() .在旋转探究活动中提出下列问题,请你帮他们解决.
.在旋转探究活动中提出下列问题,请你帮他们解决.
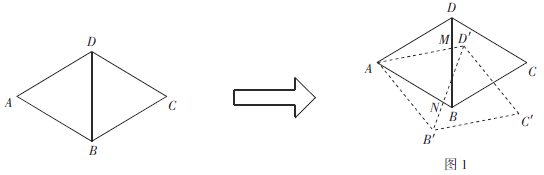
观察证明:
(1)如图1,若旋转角![]() ,
,![]() 与BD相交于点M,AB与
与BD相交于点M,AB与![]() 相交于点N.请说明线段DM与
相交于点N.请说明线段DM与![]() 的数量关系;
的数量关系;
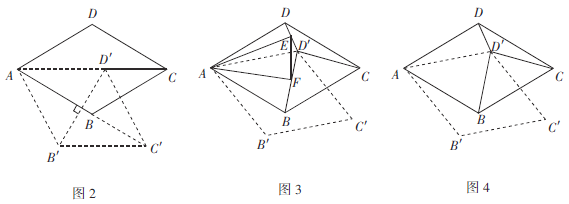
操作计算:
(2)如图2,连接![]() ,菱形ABCD旋转的过程中,当
,菱形ABCD旋转的过程中,当![]() 与AB互相垂直时,
与AB互相垂直时,![]() 的长为 ;
的长为 ;
(3)如图3,若旋转角![]() ,分别连接
,分别连接![]() ,
,![]() ,过点A分别作
,过点A分别作![]() ,
,![]() ,连接EF,菱形ABCD旋转的过程中,发现在
,连接EF,菱形ABCD旋转的过程中,发现在![]() 中存在长度不变的线段EF,请求出EF长度;
中存在长度不变的线段EF,请求出EF长度;
操作探究:
(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
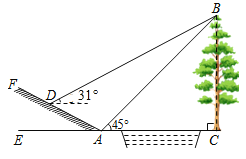
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
(1)求小明从点A走到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
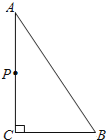
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点P(x,y)的横、纵坐标的绝对值之和叫做点P(x,y)的勾股值,记[P]=|x|+|y|.
(1)已知M(p,2p)在反比例函数y=![]() 的图象上,且[M]=3,求反比例函数的解析式;
的图象上,且[M]=3,求反比例函数的解析式;
(2)已知点A是直线y=x+2上的点,且[A]=4,求点A的坐标;
(3)若抛物线y=ax2+bx+1与直线y=x只有一个交点C,已知点C在第一象限,且2≤[C]≤4,令t=2b2﹣4a+2020,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运城有甲、乙两家葡萄采摘园的葡萄销售价格相同,中秋期间,两家采摘园推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的葡萄六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的葡萄按售价付款。优惠期间,设游客的葡萄采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() 甲(元),在乙园所需总费用为
甲(元),在乙园所需总费用为![]() 乙(元),
乙(元),![]() 甲,
甲,![]() 乙与
乙与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
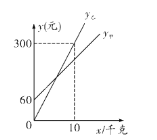
(1)求![]() 甲,
甲,![]() 乙与
乙与![]() 的函数表达式;
的函数表达式;
(2)在中秋期间,李娜一家三口准备去葡萄园采摘葡萄,采摘的葡萄合在一起支付费用,则李娜一家应选择哪家葡萄园更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com