
����Ŀ����1������̽������ͼ�������ı���ABCD�У�AB��CD��E��BC���е㣬AE�ǡ�BAD��ƽ���ߣ����߶�AB��AD��DC֮��ĵ�����ϵΪ�� ����
��2������Ǩ�ƣ���ͼ�������ı���ABCD�У�AB��CD��AF��DC���ӳ��߽��ڵ�F��E��BC���е㣬AE�ǡ�BAF��ƽ���ߣ���̽���߶�AB��AF��CF֮��ĵ�����ϵ����֤����Ľ��ۣ�
��3��������չ����ͼ����AB��CF��E��BC���е㣬��D���߶�AE�ϣ���EDF����BAE����̽���߶�AB��DF��CF֮���������ϵ����֤����Ľ��ۣ�
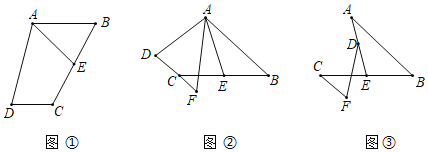
���𰸡���1��AD��AB+DC����2��AB��AF+CF��֤�������������3��AB��DF+CF��֤�����������
��������
��1�����ۣ�AD��AB+DC���ӳ�AE��DC���ڵ�F��֤����ABE�ա�FEC��AAS���������Ƴ�AB��CF����֤��DA��DF�����ɽ�����⣮
��2�����ۣ�AB��AF+CF����ͼ�����ӳ�AE��DF���ӳ����ڵ�G��֤���������ƣ�1����
��3�����ۣ�AB��DF+CF����ͼ�����ӳ�AE��CF���ӳ����ڵ�G��֤���������ƣ�1����
�⣺��1��̽�����⣺���ۣ�AD��AB+DC��
���ɣ���ͼ���У��ӳ�AE��DC���ڵ�F��

��AB��CD��
���BAF����F��
����ABE����FCE��
CE��BE����BAF����F����AEB����FEC��
���ABE�ա�FEC��AAS����
��CF��AB��
��AE����BAD��ƽ���ߣ�
���BAF����FAD��
���FAD����F��
��AD��DF��
��DC+CF��DF��
��DC+AB��AD��
�ʴ�ΪAD��AB+DC��
��2������Ǩ�ƣ����ۣ�AB��AF+CF��
֤������ͼ�����ӳ�AE��DF���ӳ����ڵ�G��

��E��BC���е㣬
��CE��BE��
��AB��DC��
���BAE����G����BE��CE����AEB����GEC
���AEB�ա�GEC��AAS��
��AB��GC
��AE����BAF��ƽ����
���BAG����FAG��
�ߡ�BAG��G��
���FAG����G��
��FA��FG��
��CG��CF+FG��
��AB��AF+CF��
��3��������չ�����ۣ�AB��DF+CF��
֤������ͼ�����ӳ�AE��CF���ӳ����ڵ�G��

��E��BC���е㣬
��CE��BE��
��AB��CF��
���BAE����G��
����AEB����GEC��
 ��
��
���AEB�ա�GEC��
��AB��GC��
�ߡ�EDF����BAE��
���FDG����G��
��FD��FG��
��AB��DF+CF��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90�㣬��D��ֱ��AB�ϵ�һ���㣨����A��B�غϣ���BE��CD��E����ֱ��AC��F��
��1����D�ڱ�AB��ʱ����̽���߶�BD��AB��AF��������ϵ����֤����Ľ��ۣ�
��2����D��AB���ӳ�����ʱ����̽���߶�BD��AB��AF��������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ����ѧ�����ձ�������һ��������ѧ�����������㾭������һ�������������������������������ǰ����ȥǧ����������ǰ������ֱ����ǰ��ȴ��һ�ٶ�ʮ��������Ŀ�ŵ���ȡ�����������ĩ�κϣ��Ӻ��ȴ��һ�ٶ�ʮ�߲�����Ŀ�ŵ���ȡ�������������ĩ�κϣ��ʵ����Σ�

��������Ҫ����������һ��ɽ��AH�ĸ߶�����B����D���������BC��DE����˵ĸ߶���3����B��D�������1000����1��=10����1��=6�ߣ�������AH��CB��DE��ͬһƽ���ڣ��ӱ��BC����123����F�����Կ�������A�ͱ�˶���C��ͬһֱ�������ӱ��ED����127����G�����Կ�������A�ͱ�˶���E��ͬһֱ���ϣ���ɽ��AH�ĸ߶���_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy��������C��һ��P����C������l����������������ڵ�P��ʱ���������������������������������l�ļнǺ��������������l�ļн��������P��Ϊ����㣮�涨�����߲��ܡ���������C��������������ڡ�C��ʱ��ֻ��Բ����з���������������ڡ�C��ʱ��ֻ��Բ�ڽ��з��䣮�ر����Բ�����߲�����Ϊ������ߺͷ�����ߣ������ڡ�C�ⷴ���ʾ��ͼ��ͼ1��ʾ�����С�1=��2��

��1���ԡ�C��һ�������������߾���C��һ�η�����ʾ��ͼ��ͼ2��ʾ��P1�ǵ�1������㣮����ͼ2���������߾���C�ڶ��η����ķ�����ߺͷ����P3��
��2������O�İ뾶Ϊ1ʱ����ͼ3��
�ٵ�һ�����ڵ�һ���������ƽ����y�������ԡ�O���ⲿ������Բ�ϵ�P�����˹��߾���O����������������x��ƽ�����������������l�ļн�Ϊ___________����
���Ե�M��0��1������������������ڡ�O��˳ʱ�뷽�ϵط��䣮����1���������P1���ڶ����������P2���Դ���������8���������P8ǡ�����M�غ������1�������P1������Ϊ___________��
��3����ͼ4����M������Ϊ��0��2������M�İ뾶Ϊ1����һ�������Ե�O������������߾���M�����������������������������������P���������ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
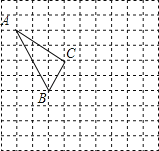
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ����4��5��������1��3����
��1������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ����עԭ���Լ�x�ᡢy�
��2��������ABC����y��ԳƵġ�A��B��C�䣬��д����B������ꣻ
��3����P��x���ϵĶ��㣬��ͼ���ҳ�ʹ��A��BP�ܳ���Сʱ�ĵ�P��ֱ��д����P�������ǣ��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯�����ʿδ�����������������������н�ʦ������Ů��ʦ���һ�Ƚ���ѧУ������������ʦ�������ѡ��λ��ʦ�μ��н�������֯�ľ�������ѡ����λ��ʦǡ����һ��һŮ�ĸ���Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̾����ı�����·ݵ��ۼ۱�һ�·�ÿ̨����500Ԫ����֪������ͬ�����ı���һ�·ݵ����۶�Ϊ9��Ԫ�����·ݵ����۶�ֻ��8��Ԫ��
��1�����·ݱ���ÿ̨�ۼ�Ϊ����Ԫ��
��2��Ϊ��������þ����̼ƻ����·��ٹ���ϴ�»��������ۣ���֪ϴ�»�ÿ̨����Ϊ4000Ԫ������ÿ̨����Ϊ3500Ԫ��Ԥ���ò�����7.6��Ԫ���ʽ������ּҵ繲20̨�������Ϊy̨��y��12���������м��ֽ���������
��3�����·�Ϊ�˴������þ����̾����ڶ��·��ۼ۵Ļ����ϣ�ÿ�۳�һ̨�����ٷ����˿��ֽ�aԪ����ϴ�»���ÿ̨4400Ԫ���ۣ���������£�����2���и�������õ�������ͬ����aӦȡ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���������Ƕ��κ���![]() ��a��0����ͼ�������н��ۣ���abc��0����b+2a=0������������x�����һ������Ϊ��4��0������a+c��b����3a+c��0��������ȷ�Ľ�����
��a��0����ͼ�������н��ۣ���abc��0����b+2a=0������������x�����һ������Ϊ��4��0������a+c��b����3a+c��0��������ȷ�Ľ�����
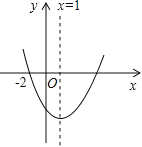
A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��Բ�ϵ����㣬��
��Բ�ϵ����㣬��![]() ƽ��
ƽ��![]() ������
������![]() ��
��![]() �ӳ��ߵĴ���
�ӳ��ߵĴ���![]() ������Ϊ
������Ϊ![]() ����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
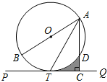
��![]() ����ͼ����Ӱ���ֵ������________��
����ͼ����Ӱ���ֵ������________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com