
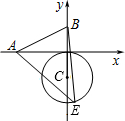
 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )| A. | 2+$\frac{\sqrt{5}}{2}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 3+$\frac{\sqrt{3}}{2}$ | D. | 4+$\frac{\sqrt{3}}{2}$ |
分析 方法一、先判断出点E的位置,点E在过点C垂直于AC的直线和圆C在点C下方的交点,然后求出直线AB解析式,进而得出CD解析式,即可得出点D坐标,再求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
方法二,先求出OA,OB,根据勾股定理得出AB,利用面积相等求出OF,再利用三角形的中位线求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
解答 解:方法一、如图,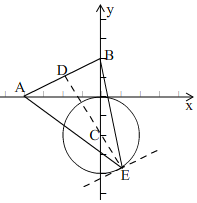 过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大),
过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大),
设直线AB的解析式为y=kx+b(k≠0),
∵A(-2,0),B(0,1),
∴$\left\{\begin{array}{l}{-2k+b=0}\\{b=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{1}{2}$x+1①,
∵CD⊥AB,C(0,-1),
∴直线CD的解析式为y=-2x-1②,
联立①②得,D(-$\frac{4}{5}$,$\frac{3}{5}$),
∵C(0,-1),
∴CD=$\sqrt{(\frac{4}{5})^{2}+(\frac{3}{5}+1)^{2}}$=$\frac{4\sqrt{5}}{5}$,
∵⊙C的半径为1,
∴DE=CD+CE=$\frac{4\sqrt{5}}{5}$+1,
∵A(-2,0),B(0,1),
∴AB=$\sqrt{5}$,
∴S△ABE面积的最大值=$\frac{1}{2}$AB•DE=$\frac{1}{2}$($\frac{4\sqrt{5}}{5}$+1)×$\sqrt{5}$=2+$\frac{\sqrt{5}}{2}$,
故选A.
方法二、如图1, 过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大,而过圆心时,和圆相交两个点,一个是最大的,一个是最小的),
过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大,而过圆心时,和圆相交两个点,一个是最大的,一个是最小的),
过点O作OF⊥AB于F,
∵A、B两点的坐标分别为(-2,0)、(0,1)
∴OA=2,OB=1,
在Rt△AOB中,根据勾股定理得,AB=$\sqrt{5}$,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OF,
∴OF=$\frac{OA•OB}{AB}$=$\frac{2\sqrt{5}}{5}$,
∵点C(0,-1),
∴OC=1,
∴OB=OC,
∴CD=2OF=$\frac{4\sqrt{5}}{5}$,
∵⊙C的半径为1,
∴DE=CD+CE=$\frac{4\sqrt{5}}{5}$+1,
∵A(-2,0),B(0,1),
∴AB=$\sqrt{5}$,
∴S△ABE面积的最大值=$\frac{1}{2}$AB•DE=$\frac{1}{2}$($\frac{4\sqrt{5}}{5}$+1)×$\sqrt{5}$=2+$\frac{\sqrt{5}}{2}$,
故选A.
点评 此题是圆的综合题,主要考查了圆的性质,待定系数法,求两条直线的交点的方法,三角形的面积公式,解本题的关键是判断出点E的位置,是一道中等难度的试题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
| 车型 | A | B |
| 载重量(吨/辆) | 3 | 4 |
| 租金(元/辆) | 1000 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
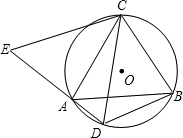 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
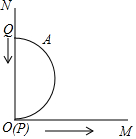 如图,己知射线OM与射线ON互相垂直,A是直径PQ为2cm的半圆铁片上一点,且弧AQ的度数为60°,(即弧AQ所对的圆心角为60°)动点P从点O沿射线OM开始滑动,同时动点Q在ON上滑动,当点Q滑至点O停止时,点A所经过的路程是( )
如图,己知射线OM与射线ON互相垂直,A是直径PQ为2cm的半圆铁片上一点,且弧AQ的度数为60°,(即弧AQ所对的圆心角为60°)动点P从点O沿射线OM开始滑动,同时动点Q在ON上滑动,当点Q滑至点O停止时,点A所经过的路程是( )| A. | 3 | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 6-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
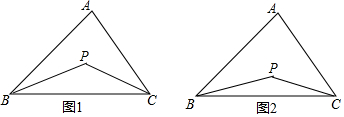 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com