练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．绝对值最小的有理数是（　　）
    A．-1B．0C．1D．不存在

    分析 根据绝对值的含义和求法，可得①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零，所以当a是正有理数和负有理数时，它的绝对值都大于0；当a是零时，a的绝对值是零，所以绝对值最小的有理数是0，据此解答即可．

    解答 解：∵当a是正有理数和负有理数时，它的绝对值都大于0；当a是零时，a的绝对值是零，
    ∴绝对值最小的有理数是0．
    故选：B．

    点评 此题主要考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

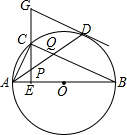    11．如图，在⊙O中．AB是直径，点D是⊙O上-点．点C是$\widehat{AD}$的中点，CE⊥AB于点E，在EC的延长线上有一点G，使GP=GD．连接AD，分别交CE、CB于点P、Q，连接AC，且AC=6，BC=8．
    （1）求证：GD是⊙O的切线；
    （2）求线段AQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知关于x的一元二次方程x2+4x+m-1=0有两个不相等的实数根．
    （1）求m的取值范围；
    （2）设x1、x2方程的两个实数根，请你为m选取一个合适的整数，求x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知关于x的一元二次方程ax2+（3a+1）x+2（a+1）=0（a≠0）
    （1）求证：无论a为任何非零实数，方程总有两个实数根；
    （2）当a取何整数时，关于x的方程ax2+（3a+1）x+2（a+1）=0（a≠0）的两个实数根均为负整数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．2015年12月，无锡市梁溪区正式成立．梁溪区包含原崇安区、南长区、北塘区，总人口近1015000人，这个人口数据用科学记数法可表示为1.015×106．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，PA是⊙O的切线，切点为A，PA=$\sqrt{3}$，∠APO=30°，则⊙O的半径为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：$\sqrt{4}$+（$\frac{1}{2}$）-1-2cos60°+（3-π）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知，如图，在平面直角坐标系中，点A坐标为（4，0），点B坐标为（0，-4），C为y轴负半轴上一点，且OC=AB，抛物线y=$\sqrt{2}$x2+bx+c的图象经过A，C两点．
    （1）求此抛物线的解析式；
    （2）将∠OAB的顶点A沿AB平移，在平移过程中，保持∠OAB的大小不变，顶点A记为A1，一边AB记为A1B1，A1与B重合时停止平移．A1B1与y轴交于点D．当△A1OD是以A1D为腰的等腰三角形时，求点A1的坐标；
    （3）在（2）问的条件下，直线A1B1与x轴交于点E，P为（1）中抛物线上一动点，直线PA1交x轴于点G，在直线EB1下方的抛物线上是否存在一点P，使得△PDA1与△GEA1的面积之比为1+2$\sqrt{2}$：1？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知菱形ABCD中，对角线AC=16，BD=12，则此菱形的高等于$\frac{48}{5}$．

    查看答案和解析>>

    同步练习册答案