
【题目】抛物线y=![]() x2-mx+
x2-mx+![]() m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
(1)若点A的坐标为(1,0)
①求抛物线的表达式;
②当n≤x≤2时,函数值y的取值范围是-![]() ≤y≤5-n,求n的值;
≤y≤5-n,求n的值;
(2)将抛物线在x轴下方的部分沿x轴翻折,得到新的函数的图象,如图,当2<x<3时,若此函数的值随x的增大而减小,直接写出m的取值范围.
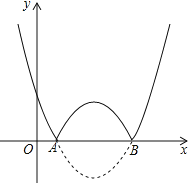
【答案】(1)①y=![]() x2-3x+
x2-3x+![]() n的值为-1;(2)1≤m≤2或m≥5.
n的值为-1;(2)1≤m≤2或m≥5.
【解析】
(1)①将点A(1,0)代入y=![]() x2-mx+
x2-mx+![]() m2-2,可求m,再求解析式;②根据所求二次函数解析式,从函数图像的变化情况得
m2-2,可求m,再求解析式;②根据所求二次函数解析式,从函数图像的变化情况得![]() n2-3n+
n2-3n+![]() =5-n,解方程可得n;(2)由y=0时,
=5-n,解方程可得n;(2)由y=0时,![]() x2-mx+
x2-mx+![]() m2-2=0,可求出点A,B的坐标,抛物线的对称轴x=-
m2-2=0,可求出点A,B的坐标,抛物线的对称轴x=-![]() =m;①当m>3时,有m-2≥3;②当m≤2时,有m+2≥3,综上所述:可得m的取值范围.
=m;①当m>3时,有m-2≥3;②当m≤2时,有m+2≥3,综上所述:可得m的取值范围.
解:(1)①将点A(1,0)代入y=![]() x2-mx+
x2-mx+![]() m2-2,得:0=
m2-2,得:0=![]() -m+
-m+![]() m2-2,
m2-2,
解得:m1=3,m2=-1(舍去),
∴抛物线的表达式为y=![]() x2-3x+
x2-3x+![]() .
.
②∵抛物线的表达式为y=![]() x2-3x+
x2-3x+![]() ,
,
∴抛物线开口向上,对称轴为直线x=-![]() =3,
=3,
∴当n≤x≤2时,y随x的增大而减小.
∵当n≤x≤2时,函数值y的取值范围是-![]() ≤y≤5-n,
≤y≤5-n,
∴![]() n2-3n+
n2-3n+![]() =5-n,即n2-4n-5=0,
=5-n,即n2-4n-5=0,
解得:n1=5(不合题意,舍去),n2=-1,
∴n的值为-1.
(2)当y=0时,![]() x2-mx+
x2-mx+![]() m2-2=0,即
m2-2=0,即![]() [x-(m+2)][x-(m-2)]=0,
[x-(m+2)][x-(m-2)]=0,
解得:x1=m-2,x2=m+2,
∴点A的坐标为(m-2,0),点B的坐标为(m+2,0).
∵抛物线的表达式为y=![]() x2-mx+
x2-mx+![]() m2-2,
m2-2,
∴对称轴为直线x=-![]() =m.
=m.
①当m>3时,有m-2≥3,
解得:m≥5;
②当m≤2时,有m+2≥3,
解得:m≥1,
∴1≤m≤2.
综上所述:m的取值范围为1≤m≤2或m≥5.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
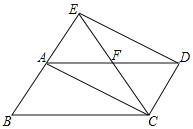
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.(1)求证:OE=CD (2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
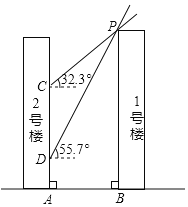
【题目】如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD沿其对角线AC折叠,使△ABC落在AEC处,CE与AD交于点F,连接DE.
(1)请你判断AC,DE的位置关系,并说明理由;
(2)若折叠后,CE平分AD,AB=4,BC=6,请利用(1)中的结论,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2与点D.已知l1与l2的距离为1,l2与l3的距离为3,则线段CD的长等于______.
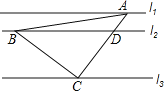
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
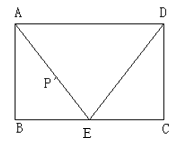
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
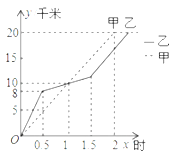
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=4,BC=3,点E为AB的中点,将矩形ABCD沿CE折叠,使得点B落到点F的位置.
(1)求证:AF∥CE.
(2)求AF的长度.
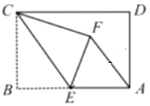
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com